Математика / 4. Прикладная математика

К.ф.-м.н. Айпанов Ш.А.

Казахский национальный университет им. аль-Фараби,

г. Алматы, Казахстан

ЭКСПОНЕНЦИАЛЬНАЯ УСТОЙЧИВОСТЬ В ЦЕЛОМ ЛИНЕЙНОЙ СИСТЕМЫ УПРАВЛЕНИЯ

1. Постановка задачи. Рассматривается линейная система управления, описываемая обыкновенным дифференциальным уравнением вида

, (1)

где – -вектор состояния объекта; – -вектор управления; , – постоянные матрицы размерностей , соответственно. Выходом системы является ‑вектор измерений

, (2)

где – постоянная -матрица. Управление системой осуществляется по каналу обратной связи с помощью сигнала вида

, (3)

где элементы -матрицы усиления являются функциями от времени. Предполагается, что система (1) является управляемой, а система (1), (2) – наблюдаемой, т.е.

(символ * означает операцию транспонирования).

Требуется найти управление вида (3), которое обеспечивает экспоненциальную устойчивость в целом системы (1).

Подставляя (3) в уравнение (1), с учетом (2) получим систему вида

. (4)

В книге [1], посвященной нерешенным проблемам теории систем и управления, Р. Брокеттом сформулирована задача о стабилизации: для заданной тройки постоянных матриц требуется найти условия, при выполнении которых существует зависящая от времени матрица такая, что линейная нестационарная система вида (4) является асимптотически устойчивой. В работе [2] получено решение проблемы Брокетта для частного случая системы второго порядка () со скалярным входом () и скалярным выходом (). В работах [3, 4] проблема Брокетта решена также для частного случая (для непрерывных и дискретных систем второго порядка со скалярным входом).

2. Вспомогательная задача. Рассмотрим линейную систему вида

, (5)

где -матрица ; симметричная -матрица , , ; – -вектор управления; числа . Для системы (5) поставим задачу минимизации квадратичного функционала

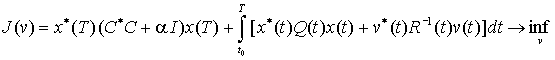, (6)

где – симметричная -матрица, ; – единичная -матрица; число . Неравенство означает, что ,

Используя принцип максимума Понтрягина, можно показать, что оптимальное управление в линейно-квадратичной задаче (5), (6) имеет вид [5]

, (7)

где сопряженный -вектор является решением следующей двухточечной краевой задачи

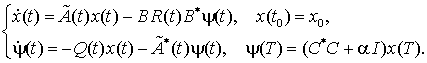(8)

Вектор может быть представлен в виде где симметричная -матрица определяется из матричного дифференциального уравнения Риккати

(9)

с конечным условием

(10)

Таким образом, оптимальное управление во вспомогательной задаче (5), (6) будет иметь вид

. (11)

Вдоль траектории , соответствующей управлению (7), рассмотрим функцию

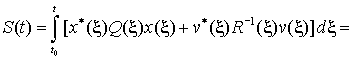
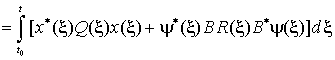. (12)

Из системы (8) имеем

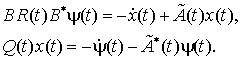(13)

Подставляя (13) в подынтегральное выражение в (12), получим

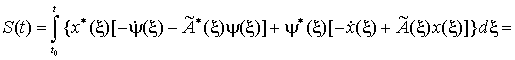
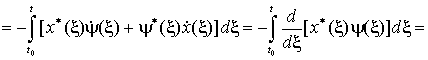
. (14)

Таким образом, из (6) с учетом (14), (10) получим, что

. (15)

Кроме того, функцию с использованием представления оптимального управления в виде (11) можно записать следующим образом:

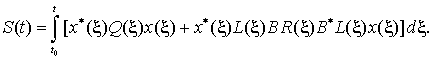
Отсюда

(16)

где симметричная -матрица удовлетворяет условию

, (17)

поскольку .

Выберем таким образом, чтобы матрица

(18)

была решением уравнения Риккати (9) (отметим, что при таком выборе матрицы конечное условие (10) будет выполнено автоматически). Из (9) имеем, что матрицу следует выбрать следующим образом:

. (19)

Предположим, что за счет выбора матрицы , , и чисел , можно добиться, чтобы матрица вида (19) удовлетворяла условию

. (20)

Итак, при выборе матрицы в виде (18) оптимальное управление (11) будет равно

. (21)

и, как следует из (15), оптимальное значение функционала (6) будет равно

. (22)

При управлении (21) дифференциальное уравнение (5) может быть представлено в виде

где

(23)

Рассматривая далее вспомогательную задачу (5), (6) в бесконечном интервале времени , приходим к выводу, что для любого заданного начального условия траектория для системы (5) при управлении вида (21) и траектория для исходной системы (1) при управлении вида (23) совпадают. Следовательно, вопрос об устойчивости решений системы (1), (23) сводится к вопросу об устойчивости решений системы (5), (21). При этом искомую матрицу усиления в управлении (3) можно представить в виде (23), где матрица и числа должны быть выбраны таким образом, чтобы выполнялось условие (20) для матрицы вида (19).

3. Экспоненциальная устойчивость в целом. Исследуем далее асимптотические свойства решений системы управления (5), (21) в бесконечном интервале времени . Пусть управление выбрано по формуле (21), а траектория является решением дифференциального уравнения

. (24)

Вдоль траектории , соответствующей выбранному управлению , рассмотрим функции

,

.

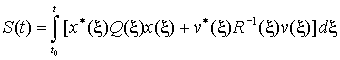Из соотношения (22) следует, что

, (25)

где .

Отметим, что является монотонно возрастающей функцией в интервале . Следовательно, функция монотонно убывает в интервале , причем она ограничена снизу: . Отсюда следует, что существует конечный предел .

Для квадратичной формы справедливы неравенства

, (26)

где – минимальное и максимальное собственные значения матрицы соответственно; . Следовательно,

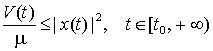. (27)

Из (25), (16) имеем, что . Для квадратичной формы в силу условия (17) имеет место оценка , , , следовательно, , или

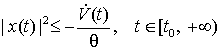. (28)

Из полученных неравенств (27), (28) следует соотношение 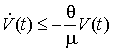, которое можно записать в виде 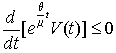. Отсюда следует, что , или

. (29)

Легко убедиться, что , следовательно, при любых начальных условиях . Из (29) с учетом неравенств (26) имеем

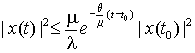, т.е. .

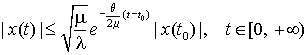Таким образом, при управлении вида (21) система (5) является экспоненциально устойчивой в целом.

4. Обсуждение результатов. Возвращаясь к задаче Брокетта о стабилизации системы (4), можно утверждать, что если матрицу выбрать в виде , где матрица , , удовлетворяет условию

для некоторых , , то линейная неавтономная система (4) будет экспоненциально устойчивой в целом.

Таким образом, в настоящей статье получены достаточные условия, при выполнении которых система (4) будет не только асимптотически устойчивой в смысле Ляпунова, но и экспоненциально устойчивой в целом (т.е. при любых начальных условиях ). Кроме того, предлагается конструктивный метод выбора матрицы , решающей проблему Брокетта.

Литература:

1. Brockett R. A stabilization problem // In: Open Problems in Mathematical Systems and Control Theory. – London: Springer, 1999. – P. 75-78.

2. Moreau L., Aeyels D. Stabilization by means of periodic output feedback // 38^th IEEE Conference on Decision and Control: Conference Proceedings. – Arisona, 1999. – P. 108-109.

3. Leonov G.A. The Brockett stabilization problem // Automation and Remote Control, vol. 62, No. 5, 2001. – P. 847-849.

4. Leonov G.A. The Brockett problem for linear discrete control systems // Automation and Remote Control, vol. 63, No. 5, 2002. – P. 777-781.

5. Ройтенберг Я.Н. Автоматическое управление. М.: Наука, 1978. – 552 с.