К.ф.м.н. Шамсуддинов Ф. и
Хусаинов.Р.
Кургантюбинский госуниверситет Республика Таджикистан
Husainov19832012@mail.ru
Переопределенной системы
первого порядка в
трехмерном случае с
граничными и внутренними
сингулярными областями.
Обозначим через
D
параллелепипед ![]()
Далее обозначим
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
В области
D
рассмотрим следующую систему
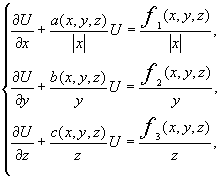 (1.1)
(1.1)
где![]() заданные функции в области
заданные функции в области ![]() .
.
Проблеме исследования переопределенных систем
с сингулярными линиями и сингулярными областями посвящено много работ. В
частности в ![]() , исследована переопределенная система первого и некоторые
случае второго порядка с сингулярными и сверхсингулярными линиями. В
, исследована переопределенная система первого и некоторые
случае второго порядка с сингулярными и сверхсингулярными линиями. В ![]() исследовано некоторые
случаи системы (1.1).
исследовано некоторые
случаи системы (1.1).
Исследованием переопределенной систем с многими
сингулярными областями посвящено
много работ, в частности
![]() .
.
По методу
разработанной в ![]() в случае, когда основным уравнением является
первое уравнение, получено следующее
утверждение.
в случае, когда основным уравнением является
первое уравнение, получено следующее
утверждение.
Теорема
1. Пусть
в системы (1.1)
коэффициенты
![]() и правые
части
и правые
части ![]()
![]()
![]() в области
D удовлетворяют следующим условиям совместности
в области
D удовлетворяют следующим условиям совместности
![]() (1.2)
(1.2)
![]() (1.3)
(1.3)
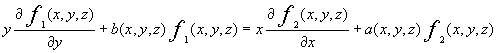 (1.4)
(1.4)
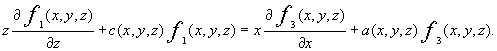 (1.5)
(1.5)
Кроме
того пусть существует
следующие пределы
![]()
![]() , (1.6)
, (1.6)
![]()
![]() (1.7)
(1.7)
Пусть
функции b(0,y,z) и c(0,y,z) удовлетворяют следующие условие совместности
![]() (1.8)
(1.8)
Функции ![]()
![]() соответственно удовлетворяют следующим условиям совместности
соответственно удовлетворяют следующим условиям совместности
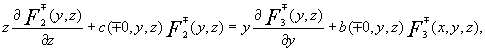 (1.9)
(1.9)
и
существует пределы
![]() . (1.10)
. (1.10)
Функции ![]()
Кроме того
эти функции удовлетворяют следующим
условиям типа Гельдера
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
![]() (1.13)
(1.13)
Далее
допустим, что
![]()
![]() и при
и при![]() a
a![]()
![]() со
следующим асимптотическим поведением
со
следующим асимптотическим поведением
![]() при
при ![]() .
.
Функции ![]() и при
и при
![]() со следующим
асимптотическим поведением
со следующим
асимптотическим поведением
![]() при
при ![]()
Функции ![]() и при
и при
![]()
![]() со следующим
асимптотическим поведением
со следующим
асимптотическим поведением
![]() , при
, при
![]()
Тогда
любое решение системы
уравнений (1) из
класса ![]() представимо в
виде
представимо в
виде
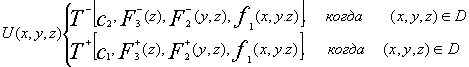 (1.14)
(1.14)
где ![]()
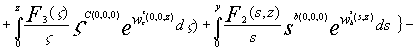
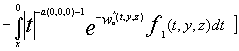 (1.15)
(1.15)
когда ![]()
![]()
![]()
![]() (1.16)
(1.16)
когда ![]() , где
, где ![]() - произвольные постоянные.
- произвольные постоянные.
Литература
1.Раджабов Н.Введение в
теорию дифференциальных уравнений
в частных производных
со сверх сингулярными коэффициентами. Душанбе,
Изд. ТГУ,1992-236с.
2.Нусрат Раджабов., Мохаммед эльсаэд
абдель-Аал. Переопределенная линейная
система второго порядка с сингулярными и сверхсингулярными линиями.LAP LAMBET Academic Publishing,Germany,2011,248p.
3.Раджабов Н., Хусаинов
Р.Ш.Переопределенная система трех дифференциальных уравнений с двумя граничными
сингулярными областями и одной внутренний сингулярной областью//Теория
дифференциальных и интегральных уравнений и их приложения (посвященной 20-й
годовщине Независимости Республика Таджикистан) Душанбе,23-24 июня
2011г.с.94-99.