Ленюк М. П.
Чернівецький факультет НТУ „ХПІ”
ГІБРИДНІ
ІНТЕГРАЛЬНІ ПЕРЕТВОРЕННЯ ТИПУ (КОНТРОВИЧА-ЛЄБЄДЄВА) – ЕЙЛЕРА –
БЕССЕЛЯ НА ПОЛЯРНІЙ ОСІ
Запровадимо методом дельта – подібної
послідовності інтегральне перетворення, породжене на множині![]() гібридним диференціальним оператором (ГДО).
гібридним диференціальним оператором (ГДО).
![]() (1)
(1)
У рівності (1) ![]() - одинична функція
Гевісайда [1];
- одинична функція
Гевісайда [1]; ![]() - диференціальний
оператор Конторовича-Лєбєдєва [2];
- диференціальний
оператор Конторовича-Лєбєдєва [2]; ![]() - диференціальний
оператор Ейлера [3],
- диференціальний
оператор Ейлера [3], ![]() - диференціальний
оператор Бесселя [4];
- диференціальний
оператор Бесселя [4]; ![]() .
.
Оскільки ГДО ![]() самоспряжений і
має дві особливі точки
самоспряжений і
має дві особливі точки ![]() та
та ![]() , то його спектр дійсний і неперервний. Можна вважати, що
спектральний параметр
, то його спектр дійсний і неперервний. Можна вважати, що
спектральний параметр ![]() . Йому відповідає комплекснозначна спектральна вектор-функція
[5].
. Йому відповідає комплекснозначна спектральна вектор-функція
[5].
![]() (2)
(2)
При цьому функції
![]()
![]() , (3)
, (3)
повинні
задовольняти відповідно диференціальні рівняння
![]()
![]() (4)
(4)
![]()
та стандартні умови спряження
![]() (5)
(5)
![]()
Фундаментальну
систему розв’язків для диференціального рівняння Конторовича-Лєбєдєва ![]() складають функції
складають функції ![]() та
та ![]() [2]; фундаментальну систему розв’язків для диференціального
рівняння Ейлера
[2]; фундаментальну систему розв’язків для диференціального
рівняння Ейлера ![]() складають функції
складають функції ![]() та
та ![]() [3]; фундаментальну
систему розв’язків для диференціального рівняння Бесселя
[3]; фундаментальну
систему розв’язків для диференціального рівняння Бесселя ![]() складають функції
складають функції ![]() та
та ![]() [4].
[4].
В
силу лінійності задачі (3) – (5) покладемо
![]()
![]()
![]() (6)
(6)
Для
знаходження 12-ти величин ![]() залучимо
дельта-подібну послідовність - ядро
Коші як фундаментальну матрицю розв’язків задачі Коші для параболічної системи
рівнянь теплопровідності, породженої ГДО
залучимо
дельта-подібну послідовність - ядро
Коші як фундаментальну матрицю розв’язків задачі Коші для параболічної системи
рівнянь теплопровідності, породженої ГДО ![]() , визначеною рівністю (1).
, визначеною рівністю (1).
Побудуємо
в області ![]() обмежений розв’язок сепаратної системи диференціальних
рівнянь параболічного типу [6]
обмежений розв’язок сепаратної системи диференціальних
рівнянь параболічного типу [6]
![]()
![]() (7)
(7)
![]()
за початковими умовами
![]() (8)
(8)
та умовами спряження
![]() (9)
(9)
Припустимо,
що вектор-функція ![]() є оригіналом за Лапласом стосовно
є оригіналом за Лапласом стосовно ![]() [7]. В зображенні за
Лапласом отримуємо крайову задачу: побудувати обмежений на множині
[7]. В зображенні за
Лапласом отримуємо крайову задачу: побудувати обмежений на множині ![]() розв’язок системи звичайних
диференціальних рівнянь Конторовича-Лєбєдєва, Ейлера та Бесселя другого порядку
для модифікованих функцій
розв’язок системи звичайних
диференціальних рівнянь Конторовича-Лєбєдєва, Ейлера та Бесселя другого порядку
для модифікованих функцій
![]()
![]() (10)
(10)
![]()
за умовами спряження
![]() (11)
(11)
У
рівностях (10), (11) ![]() ,
, ![]()
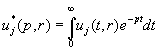 ,
, ![]() [7].
[7].
Фундаментальну
систему розв’язків для диференціального рівняння (Конторовича - Лєбєдєва) ![]() утворюють
модифіковані функції Бесселя
утворюють
модифіковані функції Бесселя ![]() та
та ![]() [2]; фундаментальну
систему розв’язків для диференціального рівняння Ейлера
[2]; фундаментальну
систему розв’язків для диференціального рівняння Ейлера ![]() утворюють функції
утворюють функції ![]() та
та ![]() [3]; фундаментальну систему розв’язків для диференціального
рівняння Бесселя
[3]; фундаментальну систему розв’язків для диференціального
рівняння Бесселя ![]() утворюють модифіковані функції Бесселя
утворюють модифіковані функції Бесселя ![]() та
та ![]() [4].
[4].
Наявність
фундаментальної системи розв’язків дає можливість побудувати загальний розв’язок
крайової задачі (10), (11) методом функцій Коші [1,3]:
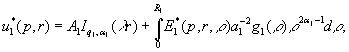
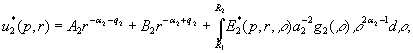 (12)
(12)
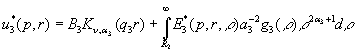
У рівностях (12) ![]() - функції Коші [1.3]:
- функції Коші [1.3]:
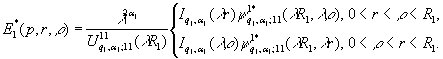 (13)
(13)
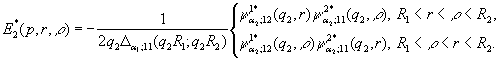 (14)
(14)
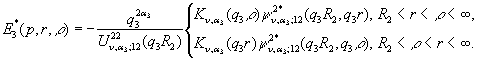 (15)
(15)
Умови спряження (11) для
визначення величин ![]() дають алгебраїчну
систему із чотирьох рівнянь:
дають алгебраїчну
систему із чотирьох рівнянь:
![]()
![]() (16)
(16)
У
системі (16) беруть участь функції
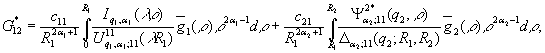
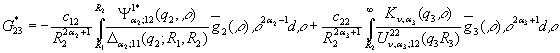 ,
,
та символ Кронекера![]() .
.
Введемо до розгляду функції:
![]()
![]()
![]()
![]()
Припустимо,
що виконана умова однозначної розв’язаності крайової задачі (10), (11): для ![]() з
з ![]() , де
, де ![]() - абсциса збіжності
інтеграла Лапласа, та
- абсциса збіжності
інтеграла Лапласа, та ![]() визначник
алгебраїчної системи (16) відмінний від нуля
визначник
алгебраїчної системи (16) відмінний від нуля
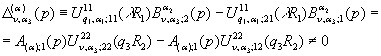 (17)
(17)
У
результаті однозначної розв’язності алгебраїчної системи (16) й підстановки
одержаних значень ![]() та
та ![]() у рівності (12) маємо
єдиний розв’язок крайової задачі (10), (11):
у рівності (12) маємо
єдиний розв’язок крайової задачі (10), (11):
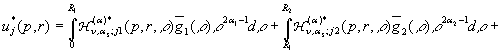
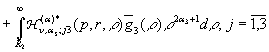 (18)
(18)
У рівностях (18) беруть участь породжені
неоднорідністю системи (16) функції впливу:
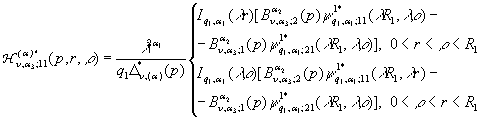
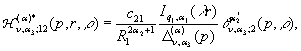
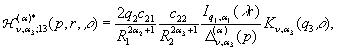
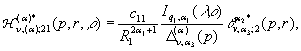
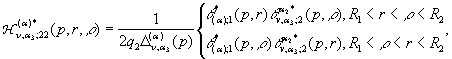 (19)
(19)
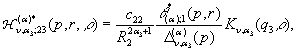
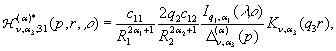
![]()
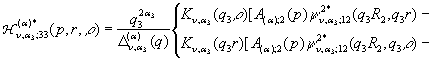
![]()
![]()
Повертаючись у рівностях (18) до оригіналу, маємо єдиний розв’язок
параболічної задачі (7) – (9):
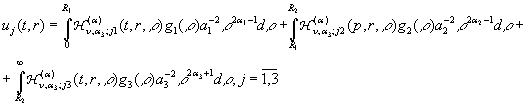 (20)
(20)
Тут за означенням [7]
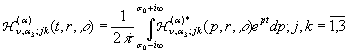 (21)
(21)
Особливими точками
функцій впливу![]() є точки галуження
є точки галуження ![]() та
та ![]() . Покладемо
. Покладемо ![]() , тобто
, тобто ![]() . Звідси знаходимо, що
. Звідси знаходимо, що ![]()
![]() ,
, ![]() . Якщо
. Якщо ![]() , то
, то ![]() якщо
якщо ![]() , то
, то ![]() якщо
якщо ![]() , то
, то ![]() ,
, ![]() .
.
Згідно методу контурного
інтегралу, леми Жордана та теореми Коші [7]
формули (21)
набувають розрахункового вигляду:
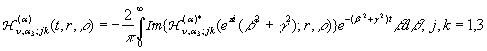 (22)
(22)
Скористаємось відомими
співвідношеннями [8,9]:
![]()
![]()
![]()
Безпосередні розрахунки
дають рівності:
![]()
![]()
![]()
![]()
![]()
Визначимо величини та
функції:
![]()
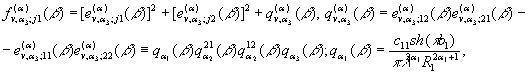
![]()
![]()
![]()
![]()
![]()
![]()
Виконавши в рівностях
(22) зазначені операції для ![]() , будемо мати рівності:
, будемо мати рівності:
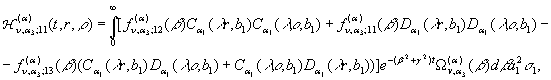 (23)
(23)
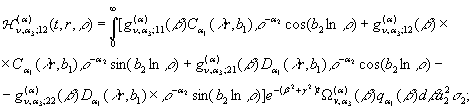 (24)
(24)
![]()
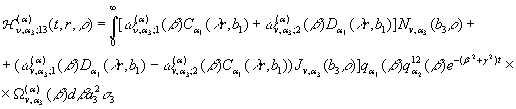 (25)
(25)
Якщо тепер вимагати
виконання рівностей
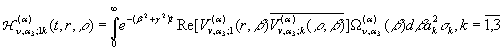 (26)
(26)
де риска зверху означає комплексне спряження, а Re(…) - дійсна частина виразу
(…), то для визначення величин ![]() одержимо алгебраїчну
систему з 11-ти рівнянь:
одержимо алгебраїчну
систему з 11-ти рівнянь:
![]()
![]() (27)
(27)
![]()
![]()
![]()
Поклавши ![]() ,знайдемо, що
,знайдемо, що
![]()
![]()
![]()
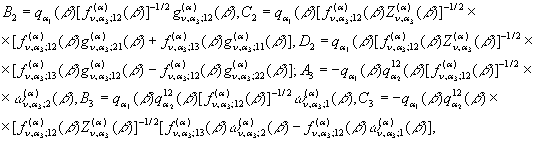
![]()
Підставимо визначені величини ![]() та
та ![]() у рівності (6). Одержимо функції:
у рівності (6). Одержимо функції:
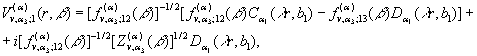 (28)
(28)
![]()
![]()
![]() (29)
(29)
![]()
![]()
![]()
![]()
Згідно формули (2) спектральна вектор-функція
визначена.
Практика показує, що із визначеними формулами (28)
– (30) функціями ![]() справджуються рівності
(26) і для
справджуються рівності
(26) і для ![]() при
при ![]() [8,9]:
[8,9]:
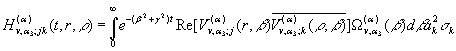 (31)
(31)
Наявність рівностей (31) дає
можливість розв’язок параболічної задачі (7)
- (9), поданий формулами (20), зобразити в такому вигляді:
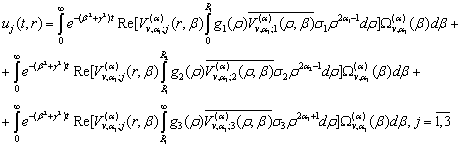 (32)
(32)
В силу початкових умов (8) та
властивостей ядра Коші як дельта-подібної послідовності з рівностей (32)
одержуємо інтегральне зображення вектор-функції ![]() з області задання ГДО
з області задання ГДО
![]() :
:
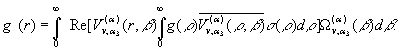 (33)
(33)
Тут бере участь вагова функція
![]()
Інтегральне зображення (33)
визначає пряме ![]() та обернене
та обернене ![]() гібридне інтегральне
перетворення, породжене на множині
гібридне інтегральне
перетворення, породжене на множині ![]() ГДО
ГДО ![]() , визначеним рівністю (1):
, визначеним рівністю (1):
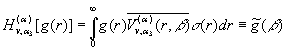 , (34)
, (34)
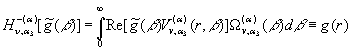 (35)
(35)
Математичним
обґрунтуванням правил (34), (35) є твердження.
Теорема 1 (про інтегральне
зображення). Якщо вектор-функція
![]()
обмежена, неперервна,
абсолютно сумовна з обмеженою варіацією на множині ![]() , то для будь-якого
, то для будь-якого ![]() має місце інтегральне
зображення (33).
має місце інтегральне
зображення (33).
Визначимо величини та функції:
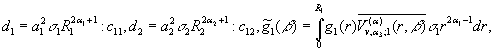
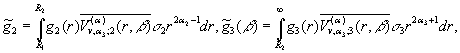
![]()
Теорема 2 (про основну тотожність).
Якщо вектор-функція ![]() неперервна на множині
неперервна на множині
![]() , а функції
, а функції ![]() задовольняють умови
обмеження
задовольняють умови
обмеження
![]()
![]()
та умови
спряження
![]() ,
,
то справджується основна
тотожність інтегрального перетворення гібридного диференціального оператора ![]() :
:
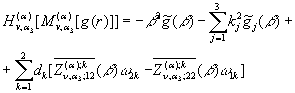 (36)
(36)
Доведення
здійснюється за логічною схемою доведення ідентичної теореми в роботі [8].
Одержані
правила (34), (35), (36) складають ефективний математичний апарат для одержання
інтегрального зображення аналітичного розв’язку відповідних здач математичної
фізики неоднорідних середовищ.
Література:
1. Шилов Г.Е. Математический
анализ. Второй специальный курс.- М.: Наука, 1965.-328с.
2. Ленюк М.П., Міхалевська Г.І. Інтегральні перетворення типу
Конторовича – Лєбєдєва. – Чернівці: Прут, 2002. – 280с.
3. Степанов В.В. Курс дифференциальных уравнений. -
М.:Физматгиз, 1959.-468с.
4. Ленюк М.П. Исследование основных краевых задач для диссипативного волнового уравнения
Бесселя. – Киев, 1983. – 62с. – (Препринт / АН УССР. Ин-т математики; 83.3).
5. Ленюк М.П., Шинкарик М.І. Гібридні
інтегральні перетворення (Фур’є, Бесселя, Лежандра). Частина1.- Тернопіль:
Економ.думка, 2004.-368с.
6. Тихонов
А.Н., Самарський А.А. Уравнения математической физики. – М.: Наука, 1972. –
735с.
7. Лавренеьев М.А., Шабат Б.В. Методы теории функций
комплексного переменного. – М.: Наука, 1987. – 688с.
8. Ленюк М.П. Гібридні інтегральні перетворення типу Ейлера – (Фур’є, Бесселя).- Чернівці:
Прут, 2009.-76с.
9. Градштейн И.С. Рыжик И.М. Таблицы
интегралов, сумм, рядов и произведений. – М.: Наука, 1971. – 1108с.