К.ф.-м.н. Аршава Е.А.
Харьковский национальный университет
строительства и архитектуры, Украина
Применение меТОДа
ОПЕРАТОРНЫХ ТОЖДЕСТВ при решении задачи ОБРАЩЕНИя ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ
1. Общая
постановка задачи и её актуальность
Изучается задача обращения некоторых новых
классов интегральных операторов методом операторных тождеств, доказывается
конечномерность соответствующих коммутационных операторов и исследуется
структура обратного оператора. Полученные результаты могут быть использованы
при решении задачи фильтрации и прогноза нестационарных случайных процессов и
сигналов.
2. Истоки
исследования автора
Настоящая работа опирается на метод [1] операторных тождеств, который Л.А.Сахнович использовал для изучения
класса уравнений вида
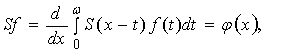 (1)
(1)
который
является наиболее общим классом уравнений с разностным ядром. Основная
идея метода состоит в доказательстве конечномерности соответствующего
интегрального оператора. В этом случае обратный оператор к данному
интегральному оператору строится при помощи функций, которые определяют
вырожденность коммутационного оператора.
3. Цели
работы
Изучение задачи обращения оператора вида
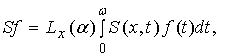 (2)
(2)
с ядром ![]() , которое удовлетворяет дифференциальному уравнению в частных
производных гиперболического типа
, которое удовлетворяет дифференциальному уравнению в частных
производных гиперболического типа
![]() (3)
(3)
4.
Используемый метод операторных тождеств
Можно доказать, что для любого
ограниченного оператора вида (2) с ядром, которое удовлетворяет условиям (3),
имеет место соотношения:
![]() где
где
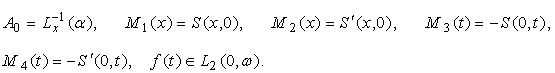
Если оператор ![]() имеет ограниченный
обратный
имеет ограниченный
обратный ![]() тогда верно представление:
тогда верно представление:
![]()
![]()
где ![]()
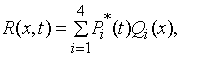 кроме того, для
кроме того, для ![]() выполняются
соотношения вида:
выполняются
соотношения вида:
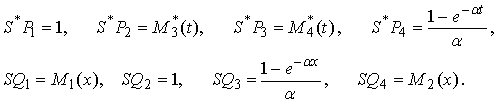 (4)
(4)
Если оператор ![]() ограничен вместе со
своим обратным и существуют функции
ограничен вместе со
своим обратным и существуют функции ![]() , которые удовлетворяют соотношениям (4), тогда для
оператора
, которые удовлетворяют соотношениям (4), тогда для
оператора ![]() имеет место
интегральное представление:
имеет место
интегральное представление:
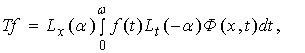
где ![]() выражается через ядро оператора
выражается через ядро оператора ![]()
![]()
Литература
1.
Сахнович Л.А. Уравнение
с разностным ядром на конечном отрезке // Успехи математических наук .– 1980. –
т.35, вып. 4 (214). - С.69-129.