ӘОЖ 512488

М. Өтемісов атындағы Батыс Қазақстан мемлекеттік университетінің Жаратылыстану және математика факультетінің математика мамандығының 2 курс магистранты Нурушева Нурзия Муратовна

Сызықтық емес оператордың туындысы

Анықтама. А сызықтық емес операторы Е₁ банах кеңістігінен Е₂ банах кеңістігіне әсер етсін. А операторы х₀ϵ Е₁ нүктесінде дифференциалданады делінеді, егер ол қандай да бір ||x-x₀||_E≤ r шарында анықталып,[1]

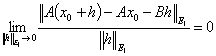(1)

болатындай, Е₁-ден Е₂-ге әсер ететін үзіліссіз сызықты В операторы бар болса.

Соңғы теңдіктегі А(х₀+h)-Ax₀ өсімшесі

А(х₀+h)-Ax₀=Bh+ω(х₀+h) (||h||≤ r) (2)

түрінде жазуға болады, мұнда ω(х₀+h)=o(||h||), яғни

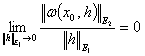. (3)

В операторын х₀ нүктесіндегі А операторының туындысы деп атайды да, А^'(х₀) арқылы белгілейді.

L₁=L_1[0,1] арқылы интегралы ақырлы болатындай х(t) өлшемді функциялардың жиыны немесе кеңістігі белгіленеді. L₁ кеңістіктің нормасы былай анықталады:

.

F(x,y,u,v) арқылы сызықты емес функциясын алайық.[2]

Осы функция арқылы (Fu)(х,у)=F(x,y,u(x),u(y)) операторын анықтауға болады. Оны F операторы дейік.

F(x,y,u,v) функциясының u және v айнымалылары бойынша дербес туындылары бар болсын.

L_{2[0,1]×[0,1]} кеңістігі 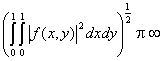шартын қанағаттандыратын f(x,y) функцияларының жиыны.

_{Олай болса, 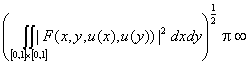орындалуы} (Fu)(х,у)=F(x,y,u(x),u(y)) операторы L_1[0,1] кеңістігінен L_{2[0,1]×[0,1]} кеңістігіне әрекеті болады.

Теорема. F(x,y,u,v) функциясымен анықталған F операторы L_1[0,1] кеңістігінен L_{2[0,1]×[0,1]} кеңістігіне әрекет етсін және u₀ϵL_1, v₀ϵL₁ нүктелерінде және туындылары болсын.

Онда әрбір hϵL₁ үшін ,

әрбір ϵL₁ үшін ,

мұндағы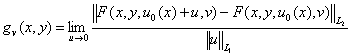

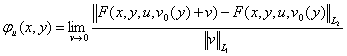
Мысал: 1) (fu)(x,y)=f(x,y,u(x,y))

(fu)(x,y)=sinⁿx²y²

(fu)(x,y)=sin uⁿ(x,y)

f '_u =n u^n-1(x,y)cos uⁿ(x,y).

2) F(x,y,u(x),v(y))=e^u(x)·v(y)

F'_u=u(y)·e^u(x)·u'(x)

F'_v=v'(y)·e^u(x).

3) ={} - вектор функциясы арқылы (u)(x)={f₁ (x,u(x)),f₂ (x,u(x))} -вектор операторын анықтайық, яғни оның әрбір координатасы сызықтық емес суперпозиция операторы. [1] әдебиетте бұл оператордың туындысын табу әдістері келтірілген. Сол нәтижелерді қолданып, осы вектор оператордың дивергенциясын анықтауға болады:

f₁(x,u(x))=e^u(x)

f₂(x,u(x))=sinⁿ u(x)

онда (u)(x)={ e^u(x); sinⁿ u(x)}

.

Әдебиеттер:

1. Красносельский М.А. и др. Интегральные операторы в пространствах суммируемых функций. - Москва, 1968-346 с

2. Ладыженский Л.А. Условия полной непрерывности интегрального оператора. - Москва, 1954-96 с