Математика/5. Математическое моделирование

Д.ф.-м.н., Байманкулов А.Т., Махамбетова Г.И.

Костанайский государственный университет им.А.Байтурсынова, Казахстан

РЕКУРРЕНТНОЕ СООТНОШЕНИЕ ДЛЯ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА КАПИЛЛЯРНОЙ ДИФФУЗИИ

Аналитическое решение задачи (6-8) из [4] не представляется возможным, поэтому нами предлагается приближенный метод с помощью которого определяется искомый коэффициент.

Для этого задается начальное приближение а следующее приближение определяется из условия монотонности функционала

. (1)

Тогда разность функционалов в соседних приближениях можно записать следующим образом

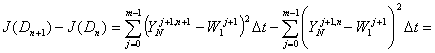
= (2)

где

Используя начально-граничные условия (7-8) из [4], перепишем разность функционалов в виде

.

Если возьмем за

тогда имеет место

. (3)

Ранее мы приняли, что разность соседних значений приближений

.

Поэтому соотношение

.

можно использовать в качестве рекуррентной формулы для вычисления коэффициента диффузии.

Для подтверждения рекуррентного соотношения потребуются доказательства ограниченности величин и .

Эти доказательства будут приведены далее методами априорных оценок решений прямой и сопряженной задач.

Литература

1.Нерпин С.В., Юзефович Г.И. О расчете нестационарного движения влаги в почве// Доклады ВАСХНИЛ, № 6, 1966.

2.Юзефович Г.И., Янгарбер В.А. Исследование нелинейного уравнения влагопереноса. // Л.: Колос. Сб. трудов по агрофизике, вып. № 14, 1967.

3.Байманкулов А.Т. Определение коэффициента капиллярной диффузии.// Материали за VIII международна научна практична конференция «Бъдещето въпроси от света на науката -2012», т.36, 17-25 декември, 2012, София.

4. Байманкулов А.Т. Априорные оценки сопряженной задачи.//Materialy IX mezinarodni vedecko-prakticka conference «Veda a technologie: krok do budoucnosti-2013», 27 unora-05 brezen 2013 roku, Praha.