Организация учебного процесса при обучении решению задач линейного программирования

В.В.Подгорная

г. Минск, Учреждение образования Федерации профсоюзов Беларуси «Международный институт трудовых и социальных отношений»

Для получения высокого результата в обучении решению задач линейного программирования преподаватели могут применять в своей работе методы и приёмы преподавания, которые активизируют фантазию студентов, побуждают увидеть необычное в привычном .Один из возможных вариантов – это комбинированное использование традиционного метода решения задач и метода «мозгового штурма».

Наиболее эффективно такой подход можно использовать при решении задач линейного программирования. Рассмотрим основные этапы работы над задачей при таком подходе в обучении. Разделим решение задачи на основные шаги. Каждый студент в группе получает карточку на которой записана решение задач. Решение может быть как правильным, так и не правильным. Каждый студент получает столько карточек – сколько этапов в решении задачи. Работы в группе состоит в том, что студенты обсуждают предложенные им варианты решений и совместно выбирают верный этап решения.

I этап. Определение цели. Анализ условия задачи.

II этап. Формулировка ожидаемого результата. На какие вопросы задачи необходимо ответить.

III этап. Подробное повторение алгоритма решается задачи. Повторение основных элементов теории.

IV этап. Работа в группах, под руководством консультанта. Из предложенных вариантов решения каждому студенту, группа должна выбрать правильный.

V этап. Составление полного правильного решения задачи группой студентов.

VI этап. Защита полученного решения.

Трудность решения задачи линейного программирования заключается в том, что не все модели задач можно свести к равносильным моделям с двумя переменными. Наиболее популярным методом решения задач линейного программирования является симплекс-метод. В основу симплекс-метода положена идея рассмотрения только крайних точек области допустимых решений задачи, а не все множество точек.

При решении задач симплекс-методом рассматривается последовательное изучение планов решения. Суть метода состоит в том, что в начале получают допустимый план, который удовлетворяет всем ограничениям, но он не обязательно является оптимальным и называется этот план начальное спорное решение. Оптимальность плана достигается последовательным улучшением начального опорного решения.

Начальный опорный план решения и составление всех последующих планов выполняют на основе метода Жордано-Гауса для системы линейных уравнений в канонической форме, в которой должна быть записана задача. Результат каждой итерации удобно записывать в виде симплексной таблицы, переход от одной таблицы к другой происходит на основе исходной задачи.

Рассмотрим применение предложенного метода на примере конкретной задачи линейного программирования.

Задача. Предприятие выпускает четыре вида продукции П₁, П₂, П₃, П₄. Для производства продукции оно располагает тремя ресурсами, запасы которых ограничены величинами 35, 30 и 40 единиц. Удельные затраты на единицу продукции и цена единицы готовой продукции заданы в виде таблицы

Ресурсы	Расходы ресурсов на единицу продукции
	П1	П2	П3	П4
Р1	4	2	2	3
Р2	1	1	2	3
Р3	3	1	2	1
Цена (ден. ед.)	14	10	14	11

Требуется определить производственную программу предприятия, которая обеспечивает максимальный доход.

I этап. Студенты в группах, под руководством консультанта анализируют условие задачи. Выделяют данные и искомые величины задачи, конкретизируют требование (вопрос) задачи.

II этап. Обучаемые повторяют основные теоретические положения, необходимые для решения задачи. Это может быть коллективная работа под руководством консультанта, работа в парах, индивидуальная работа, итогом которой может быть экспресс-тестирование, предложенное преподавателем. Выбор формы работы зависит от уровня подготовленности студентов.

Повторение теоретического материала может быть организовано в различных формах.

1. Алгоритм составления таблицы S_i-I. Для повторения поставленного вопроса студенты могут воспользоваться материалами лекций или другой литературой. Так же можно предложить заранее заготовленный теоретический материал на карточках или доске

2. Симплексное преобразование после выбора разрешающего элемента при табличных записях выполняется по следующим правилам:

1) Разрешающий элемент a_rk заменяют обратной величиной

2) Остальные элементы разрешающей строки делятся на разрешающий элемент

3) Остальные элементы разрешающего столбца делятся на разрешающий элемент и знак меняется на противоположный

4) Остальные элементы таблицы преобразовываются по правилу прямоугольника: искомый элемент равен разности произведений элементов главной и побочной диагоналей, деленной на разрешающий элемент (по воображаемому прямоугольнику пересчета) ;

Таким образом, получается новый опорный план задачи в следующей симплексной таблице. А для того, чтобы определить является ли новый опорный план оптимальным, необходимо знать следующие признаки:

a) Если все оценки индексной строки (строки целевой функции) не отрицательны, то соответствующий план является оптимальным в задаче максимилизации.

b) Если все оценки индексной строки не положительны, тол соответствующий план является оптимальным в задаче минимизации.

III этап. Составить математическую модель задачи.

Каждый студент подгруппы получает карточку, на которой прописан данный этап решения задачи, только на одной карточке записано верное решение.

Карточка №1.

Составим математическую модель задачи. Пусть x₁, x₂, x_3, x₄ – искомые объемы производства продукции, f – предприятия от производства и реализации всей продукции, который с учетом обозначений определяется следующий функций

Ограничения по используемым ресурсам примет вид:

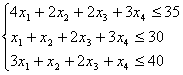
По смыслу задачи объемы продукции не могут быть отрицательны, поэтому

Карточка №2.

Составим математическую модель задачи, пусть x₁, x_2, x₃, x₄ – искомые объемы производства продукции, f – доход предприятия от производства и реализации всей продукции, который с учетом введенных обозначений определятся следующей функций

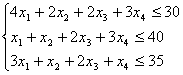
По смыслу задачи объемы не могут быть отрицательны

Мы привели пример карточек, на которых указаны правильный ход решения задачи. Очевидно, что только у одного студента карточка с правильным ходом решения. Каждый студент должен определить правильность записанного решения на своей карточке и защитить свою позицию в группе. После коллективного обсуждения консультант выбирает карточку с правильным решением. Таким образом, студенты выбрали решение задачи на данном этапе.

IV этап. Необходимо выделить начальный базис системы, т.е. выделить базисные переменные. Базисных переменных должно быть столько, сколько ограничений системы линейных уравнений, т.е. в нашем случае их должно быть три.

Наши дополнительные переменные x₅, x₆, x₇ и будут базисными, так как им соответствуют единичные векторы, которые образуют базис в трехмерном пространстве. Необходимо выразить эти переменные. Студентам предлагаются карточки следующего содержания:

Карточка №1

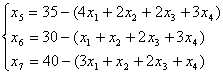
Данная карточка содержит правильное решение. Приведем пример карточки с неверным решением.

Карточка №2

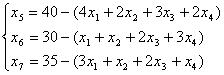
Студенты выполнив работу, аналогичную работе на предыдущем этапе выбирают правильное решение.

V этап. Заносим условие задачи в симплексную таблицу

Таблица

БП	1	СП
		-x1	-x2	-x3	-x4
x5=	35	4	2	2	3
x6=	30	1	1	2	3
x7=	40	3	1	2	1
f	0	-14	-10	-14	-11

Мы выбираем таблицу с правильно записанными числовыми данными. После обсуждения и выбора правильной таблицы студенты определяют разрешающий столбец и разрешающую строку в таблице, а так же определяют разрешающий элемент. После этого таблица принимает вид:

БП	1	СП
		-x1	-x2	-x3	-x4
x5=	35	4	2	2	3
x6=	30	1	1	2	3
x7=	40	3	1	2	1
f	0	-14	-10	-14	-11

Наша задача подобрана таким образом, что студенты могут выбрать два пути решения, т.к. в строке целевой функции два одинаковых наименьших значения равных – 14. В этом случае они должны сравнить полученные окончательно решения и выбрать из них оптимальное.

Анализируя таблицу S_i-I мы видим, что в индексной строке присутствуют отрицательные коэффициенты, поэтому данный спорный план не является оптимальным. Будем улучшать его, переходя от одного базиса к другому. Пользуясь алгоритмом решения подобных задач составим следующую таблицу. Таблицу S_i-II студенты будут получать в зависимости от выбора таблицы S_i-I. Мы показываем правильный вариант.

S_i-II

БП	1	СП				min
		-x5	-x2	-x3	-x4
X1
X6
X7			–
f

Анализируя полученные результаты, мы видим, что пока еще не получен оптимальный план, так как не все оценки строки целевой функции принимают неотрицательные значения. Значит, заполняем таблицу S_i-III.

S_i-III

БП	1	СП				min
		-x5	-x2	-x6	-x4
X1
X3
X7			–
f			–

Еще раз проводя преобразования с элементами данной таблицы мы получим оптимальный план, который находится в таблице S_i-IV.

S_i-IV

БП	1	СП
		-x5	-x1	-x6	-x4
X2	5	1	3	-1	0
X3	12,5	-0,5	-1	1	1,5
X7	10	0	2	-1	-2
f	225	3	2	4	10

И так, в k индексной стоке последней таблицы нет ни одного отрицательного элемента, следовательно, содержащийся в ней план является оптимальным. Выпишем его, зная, что значения базисных переменных находятся в столбце свободных коэффициентов, а все свободные переменные равны нулю. Получаем x₂=0; x₃=12.5; x₇=10; x₅=0; x₁=0; x₆=0; x₄=0 или план .Значение целевой функции равно 225. Но наша задача с экономически содержанием, поэтому студент должен проанализировать полученные результаты и сформулировать выводы.

Правильный вывод должен быть сформулирован следующим образом: предприятию по оптимальному плану следует производить 5 единиц продукции П₂, 12,5 единиц – П₃, продукцию П₁ и П₄ выпускать не следует, при этом ресурсы Р₁ и Р₂ будут израсходованы полностью, а ресурс Р₃ останется в количестве 10 единиц. Выручка предприятия при этом составит 225 денежных единиц.

Из всех составленных решений студенты должны выбрать правильное решение, и защитить его.

Сделаем вывод: использование такого подхода в решении задач по высшей математике при обучении экономистов способствует развитию профессиональных компетенций у студентов в данном случае это применение математического аппарата в специальной подготовке в решении экономических задач математическими методами, а также содействует развитию умения саморегуляции, самоконтроля, самодисциплины, самопознания и рефлексии.

Литература

1. Малыхин В. Л. Математика в экономике. — М.: ИНФРА-М, 2001.

2. Розен В. В. Математические модели принятия решений в экономике. — М.: Книжный дом «Университет». Высш. шк., 2002

3. Солодовников А. С., Бабайцев В. А., Браилов А. В. Математика в экономике. В 2-х ч. — М.: Финансы и статистика, 2001