Педагогические науки/5.Современные методы преподавания

Новиков В.Н.,

доцент ВАК;

Калакова Г.К.,

ст. преподаватель кафедры информатики и математики, Костанайский государственный университет им. А. Байтурсынова

Псевдорешения задач по физике

Псевдорешениями в методической литературе принято считать такие решения, которые при кажущейся верности, приводят к неверным результатам. Такие решения чаще всего выполняются учениками при рассмотрении комбинированных нестандартных задач, особенно задач повышенной трудности, предлагавшихся им на различных конкурсах, олимпиадах разного уровня.

Рассмотрим сказанное на следующих примерах.

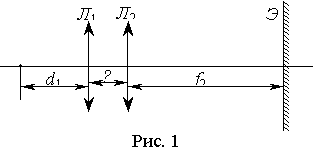
Задача 1. Объектив проекционного аппарата состоит из двух линз с фокусными расстояниями 20 см и 10 см. Расстояние между оптическими центрами линз 5 см. Какое увеличение даёт объектив при проецировании изображения на экран на расстоянии 5 м?

Ученики сразу находят оптическую силу объектива проекционного аппарата:

D = D₁ + D₂ = (5 +10) дптр = 15дптр.

Увеличение проекционного аппарата определяют по формуле:

Г = f/d = f/F – 1= f D – 1.

Беря f =5,025 м ( расстояние от центра системы линз до экрана), получают Г ≈ 74. Ответ неверный.

Неверным он получается и при f = 5 м: тоже Г = 74.

Ошибочность решения учеников заключается в том, что они использовали формулу оптической силы двух тонких сложенных вплотную линз для системы двух линз, достаточно отдаленных друг от друга.

Верным будет следующее решение.

Пусть F₁ = 20см, F₂ =10см, l =5см и f₂ =5м = 500см. Увеличение системы линз

Г = Г₁ * Г₂ = (f₁ / d₁ ) * (f₂ / d₂). (1)

Выполним схематический рисунок и некоторые обозначения на нём (рис.1).

Из формулы линзы следует:

1/d₂ =1/F₂ – 1/f₂ = 49/500,

откуда

d₂ =500/49 см ≈ 10,2 см.

Это больше, чем l. Значит изображение, даваемое первой линзой и являющееся предметом для второй линзы, мнимое, и тогда

f₁ = - (500/49 – 5) см = -( 255/49) см.

Теперь найдём

d₁. 1/d₁ =1/F₁ – 1/f₁ = 1/20 – 1* 49/(-255) = 61,75/255 = 4,13.

Подставив все полученные значения в формулу (1), получим:

Г = 61,75 ≈ 62.

Если принять F₁ =10 см, а F₂ =20 см, получим d₂ =20,8 cм; f₁ =-15,8 cм; d₁ =6,13 см. И снова Г ≈ 61,8 cм ≈ 62 см.

Задача 2. При подготовке игрушечного пистолета к выстрелу пружину жёсткостью 32 Н/м сжали на 5 см. Какую скорость приобретёт пуля массой 20 г при выстреле в вертикальном направлении?

Для решения задачи ученики используют закон сохранения и превращения энергии:

kx²/2 = mv²/2

и получают

Но ответ к задаче – 1,7м/с.

При решении ученики проявили невнимательность и не учли направление стрельбы. В действительности потенциальная энергия пружины превращается в потенциальную энергию пули, поднятой пружиной на высоту h=x, и её кинетическую энергию:

kx²/2 = mgx + mv²/2.

После решения этого уравнения получаем:

v = 1,7 м/с.

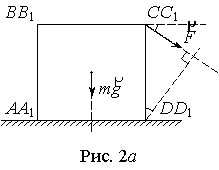Задача 3. Кубик массой 8 кг лежит на сильно шероховатой поверхности. Какую минимальную силу нужно приложить к верхней грани куба, чтобы он начал поворачиваться?

Решение ученики начинают обычно с рассмотрения очевидной для них ситуации: чтобы перевернуть кубик, вращая его относительно ребра DD₁, надо приложить силу к ребру СС₁ (рис.2а).

По условию равновесия кубика (пусть его ребро будет равно а) относительно оси DD₁ имеем: F а cos a ≥ m g а /2, откуда в предельном случае имеем: F = m g / (2cos a).

При a = 0 значение силы минимально и равно m g/2 = 40 Н.

Но в ответе F = 28,2 Н.

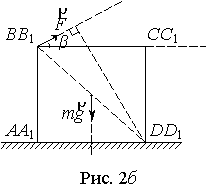
Здесь ученики не учли, что вращение кубика относительно ребра DD₁ можно осуществить, прикладывая силу и к ребру ВВ₁ той же верхней грани под углом β, (рис.2б).

В этом случае

F a√2 sin (45⁰ + β) ≥ m g a /2 ,

а в пределе получим: F=m g/(2√2sin(45⁰+ β)).

Значение силы будет минимальным и равным 28,2 Н при β = 45⁰.

Задача 4. Для изобарного нагревания газа, количество вещества которого 800 моль, на 500 К ему сообщили количество теплоты 9,4 МДж. Определить работу газа и приращение его внутренней энергии.

Видимо, «работая» до этого только с одноатомным газом, ученики сразу определяют изменение внутренней энергии газа:

МДж

Работа газа

Эти значения не совпадают с ответами к задаче: 6,1 МДж и 3.3 МДж соответственно.

Когда они посчитали для двухатомного газа, то также получили значения, не совпадающие с ответами: 8,3 МДж и 1,1 МДж.

А для трёхатомного газа результат вообще привёл их в недоумение. Оказалось, что изменение внутренней энергии газа

МДж

что больше сообщённого газу количества теплоты – 9,4 МДж.

Все решения учеников оказались неуспешными, потому что они были невнимательны к прочтению условия задачи, где речь идёт не о конкретном газе (идеальном, реальном одноатомном или двухатомном) и в вопросительной её части требуется найти «работу газа и приращение его внутренней энергии».

Работу газа или смеси газов независимо от концентрации её компонентов можно определить по формуле. С учётом уравнения состояния газа (уравнения Менделеева - Клапейрона) для изобарного процесса получим: