Физика /1.Теоретическая физика
Калакова
Г.К.,
Костанайский государственный
университет им. А. Байтурсынова, Казахстан;
к.ф-м.н. Кравцов В.М.,
г.Санкт-Петербург, Россия;
к.ф-м.н Калаков Б.А.,
Костанайский
государственный педагогический институт,
Казахстан
Решение задачи о вписании четырёхугольника
минимального периметра по методу Шварца
Ради иллюстрации применения метода Шварца в
решении задач о бильярдных траекториях рассмотрим решение задачи о вписании
четырёхугольника минимального периметра по этому методу. Мы изложим известное
решение задачи по этому методу (см., например, [1], [2], [3]) , а также
покажем, что метод позволяет коротко и просто установить формулу наименьшего
периметра вписанного четырёхугольника.
Итак, пусть дан четырёхугольник ![]() , удовлетворяющий условию, что его вершины лежат на одной
окружности. Пусть искомым вписанным в него многоугольником минимального
периметра будет
, удовлетворяющий условию, что его вершины лежат на одной
окружности. Пусть искомым вписанным в него многоугольником минимального
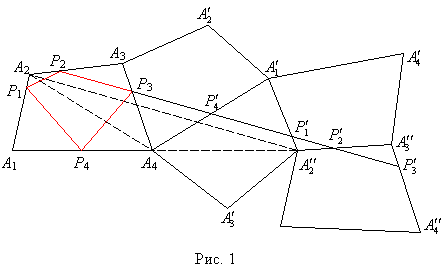
периметра будет ![]() (рис. 1). Для
четырёхугольника
(рис. 1). Для
четырёхугольника ![]() четырёхугольник
четырёхугольник ![]() должен быть
бильярдной траекторией. Последовательно проведём четыре следующих построения.
Построим четырехугольник
должен быть
бильярдной траекторией. Последовательно проведём четыре следующих построения.
Построим четырехугольник ![]() , симметричный с
, симметричный с ![]() относительно стороны
относительно стороны ![]() , затем – четырёхугольник
, затем – четырёхугольник ![]() , симметричный с
, симметричный с ![]() относительно
относительно ![]() , четырёхугольник
, четырёхугольник ![]() , симметричный с
, симметричный с ![]() относительно
относительно ![]() , и, наконец, четырёхугольник
, и, наконец, четырёхугольник ![]() , симметричный с
, симметричный с ![]() относительно
относительно ![]() .
.
Заметим, что
четырёхугольник ![]() можно получить из
четырёхугольника
можно получить из
четырёхугольника ![]() двумя поворотами:
сначала поворотом вокруг точки
двумя поворотами:
сначала поворотом вокруг точки ![]() на угол
на угол ![]() и последующим
поворотом вокруг точки
и последующим
поворотом вокруг точки ![]() на угол
на угол ![]() . Так как
. Так как ![]() , то соответственные стороны четырёхугольников
, то соответственные стороны четырёхугольников ![]() и
и ![]() параллельны. Другими
словами, четырёхугольник
параллельны. Другими
словами, четырёхугольник ![]() получен из
четырёхугольника
получен из
четырёхугольника ![]() параллельным переносом.
параллельным переносом.
В силу того, что четырёхугольник ![]() является бильярдной
траекторией, он, по проведенным построениям, разворачивается в прямолинейный
отрезок
является бильярдной
траекторией, он, по проведенным построениям, разворачивается в прямолинейный
отрезок ![]() , состоящий из отрезков
, состоящий из отрезков ![]() ,
, ![]() ,
, ![]() и
и ![]() . Как видим, итогом четырёх симметрий явился параллельный
перенос четырёхугольника
. Как видим, итогом четырёх симметрий явился параллельный
перенос четырёхугольника ![]() с вектором переноса
с вектором переноса![]() , длина которого равна периметру четырёхугольника
, длина которого равна периметру четырёхугольника ![]() . Ясно и построение четырёхугольника
. Ясно и построение четырёхугольника ![]() . Выбрав, например, произвольно точку
. Выбрав, например, произвольно точку ![]() на стороне
на стороне ![]() , строим соответственную ей точку
, строим соответственную ей точку ![]() на стороне
на стороне ![]() четырёхугольника
четырёхугольника ![]() . Соединив точки
. Соединив точки ![]() и
и ![]() прямолинейным
отрезком и получив точки
прямолинейным
отрезком и получив точки ![]() ,
, ![]() ,
, ![]() , построим на сторонах четырёхугольника
, построим на сторонах четырёхугольника ![]() точки
точки ![]() и
и ![]() , соответственные точкам
, соответственные точкам ![]() и
и ![]() .
.
Из факта, что точка ![]() была выбрана на
стороне
была выбрана на
стороне ![]() произвольно, следует,
что существует бесчисленное множество вписанных в
произвольно, следует,
что существует бесчисленное множество вписанных в ![]() четырёхугольников
минимального периметра. Соответственные стороны этих четырёхугольников
параллельны.
четырёхугольников
минимального периметра. Соответственные стороны этих четырёхугольников
параллельны.
При проведённых преобразованиях всякий вписанный
четырёхугольник, не являющийся бильярдной траекторией, развернется в ломаную,
расстояние между концами которой равно длине вектора параллельного переноса ![]() . Ясно, что периметр такого вписанного четырёхугольника, не
являющегося бильярдной траекторией, больше периметра четырёхугольника
. Ясно, что периметр такого вписанного четырёхугольника, не
являющегося бильярдной траекторией, больше периметра четырёхугольника ![]() .
.
Так как минимальный периметр вписанного многоугольника
равен длине вектора переноса итогового преобразования, то для его определения
достаточно воспользоваться расстоянием, на которое переместилась какая-либо
точка четырёхугольника ![]() при указанном
преобразовании. Рассмотрим, например, перемещение
при указанном
преобразовании. Рассмотрим, например, перемещение ![]() точки
точки ![]() . Величину отрезка
. Величину отрезка ![]() определим из
равнобедренного треугольника
определим из
равнобедренного треугольника ![]() , боковая сторона которого равна диагонали
, боковая сторона которого равна диагонали ![]() четырёхугольника
четырёхугольника ![]() , а угол при вершине равен
, а угол при вершине равен ![]() . Действительно, точка
. Действительно, точка ![]() , являющаяся образом точки
, являющаяся образом точки ![]() при проведенных
преобразованиях, может быть получена из точки
при проведенных
преобразованиях, может быть получена из точки ![]() поворотом диагонали
поворотом диагонали ![]() около точки
около точки ![]() на угол
на угол ![]() . Отсюда находим:
. Отсюда находим:
![]() =
=![]() .
.
Таким образом,
периметр четырёхугольника ![]() определён.
определён.
Литература:
1.
Адамар Ж. Элементарная
геометрия. Ч. I. Четвёртое русское издание, с
приложением составленных проф. Пчёлкиным Д. И. решений всех помещённых в тексте
задач. – М.: Учпедгиз, 1957.
2.
Радемахер Г. и Теплиц О.
Числа и фигуры. Опыты математического мышления. Пер. с нем. Контовта В. И. Под
ред., с доп. и примечаниями Яглома И. М.
–
М.: Физматгиз, 1962.
3.
Шклярский
Д. О., Ченцов Н. Н., Яглом И. М. Геометрические неравенства и задачи на
максимум и минимум. – М.: Наука, 1970.