Физика /1.Теоретическая физика
Калакова Г.К.,
Костанайский
государственный университет им. А.
Байтурсынова, Казахстан;
к.ф-м.н. Кравцов В.М.,
г.Санкт-Петербург, Россия;
к.ф-м.н Калаков Б.А.,
Костанайский государственный педагогический институт, Казахстан
Квадрат изометрии.
Траектория с двойным обходом сторон многоугольника
Теорема. В выпуклом многоугольнике с нечётным
числом сторон 
, имеющем вписанный многоугольник минимального
периметра, существует бесконечно много замкнутых бильярдных траекторий с 
парами
звеньев; звенья каждой пары параллельны одной из соотвествующих сторон
вписанного многоугольника и равно от нее удалены, расстояние между
параллельными звеньями постоянно для всех пар. Длина траектории равна
удвоенному периметру вписанного многоугольника.
Траекторию, о которой идёт речь в теореме, будем
называть траекторией с двумя обходами сторон многоугольника.
Существование бильярдной траектории с двумя обходами
сторон многоугольника установим на примере треугольника.
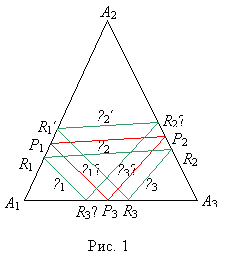Пусть в треугольник 
вписан треугольник минимального периметра 
(на рис. 1 изображен красным цветом). Стороны
треугольника 
пусть лежат соответственно на прямых 
. Обозначим, как и
прежде, симметрии относительно прямых 
,
,
соответственно через 
.
Построим в треугольнике 
замкнутую бильярдную траекторию следующим
образом. Выберем на стороне 
треугольника 
точку 
, не совпадающую с
точкой 
, и проведём через неё прямую 
параллельно 
. Применим к прямой 
преобразование симметрии 
. Получим прямую 
, пересекающую стороны
треугольника 
в точках 
и 
. Так как прямые 
и 
параллельны, то вследствие свойств
преобразования осевой симметрии параллельны и прямые 
и 
. При преобразовании
осевой симметрии сохраняется и расстояние между параллельными прямыми. Далее
найдём, что прямая 
параллельна прямой 
и удалена от неё на такое же расстояние как и
от 
. Применив к прямой 
преобразование 
, получим прямую 
:
.
Так как 
является осью скользящей симметрии 
и прямая 
параллельна 
, то и прямая 
параллельна 
и удалена от неё на то же расстояние, что и
прямая 
. Ясно, что прямые 
и 
расположены по разные стороны от прямой 
.
Аналогичные заключения можно сделать и о прямых 
,
, 
, а также о прямых 
, 
, 
. Пересекаясь со
сторонами треугольника 
, прямые 
, 
, 
,
, 
, 
образуют шестизвенную замкнутую траекторию 
.
Замечая, что, например, четырёхугольник 
является трапецией, а отрезок 
- её средней линией, можно легко установить
высказанное в теореме утверждение о длине траектории.
Отметим, что прямые 
и 
инвариантны относительно преобразования 
:
=
,
=
.
прямые
и 
инвариантны относительно преобразования 
=
, а прямые 
и 
- относительно преобразования 
=
.
Эти изометрии, относительно которых инвариантны прямые
, 
, 
, 
, 
, 
, как квадраты
скользящих симметрий 
, 
, 
, являются
параллельными переносами.
При построении траектории 
точка 
на стороне 
треугольника 
была выбрана произвольно.1)
Отсюда, очевидно, следует, что в треугольнике существует бесконечно много
траекторий подобного типа.
Множество таких траекторий имеет мощность континуума.
Рассуждения, проведённые для остроугольного
треугольника, могут быть повторены для многоугольника с любым нечётным 
, допускающего вписание
в него многоугольника минимального периметра.
Об обсуждаемой в данном разделе замкнутой траектории с
двумя обходами сторон многоугольника будем говорить, что она сопутствует
траектории, являющейся вписанным многоугольником минимального периметра. Во
всяком многоугольнике с нечётным 
, допускающем вписание
многоугольника минимального периметра, таких замкнутых самопересекающихся
траекторий бесконечно много. Изложенная теорема иллюстрируется рис. 2 и 3. На
рис. 2 и 3 показаны соответственно для пятиугольника и правильного семиугольника
вписанные многоугольники минимального периметра, а также замкнутые бильярдные
траектории.