Физика /1.Теоретическая физика

Калакова Г.К.,

Костанайский государственный университет им. А. Байтурсынова, Казахстан;

к.ф-м.н. Кравцов В.М.,

г.Санкт-Петербург, Россия;

к.ф-м.н Калаков Б.А.,

Костанайский государственный педагогический институт, Казахстан

Замкнутые бильярдные траектории в прямоугольнике и фигуры Лиссажу

Замкнутые бильярдные траектории в прямоугольнике имеют сходство с так называемыми фигурами Лиссажу. Фигурой Лиссажу называют замкнутую траекторию частицы, участвующей в двух гармонических колебаниях вдоль взаимно перпендикулярных прямых. Для описания указанных гармонических колебаний введём в рассмотрение прямоугольную систему координат, вдоль осей которой совершаются колебания частицы. Координаты и частицы, участвующей в колебаниях, пусть меняются со временем по гармоническому

закону:

,

,

где и – частоты соответствующих колебаний, и – амплитуды колебаний, – сдвиг фаз колебаний.

Как известно, траектория колеблющейся частицы замыкается только в случае, когда частоты и находятся в некотором рациональном отношении:

, (1)

где и – целые числа.

Сходство замкнутых бильярдных траекторий в прямоугольнике и фигур Лиссажу можно установить, если обратиться к кинематическим соображениям о бильярдных траекториях.

Введем прямоугольную систему координат и для описания движения бильярдного шара внутри прямоугольника. Вдоль стороны направим ось , вдоль стороны – ось .

Разложим движение бильярдного шара на два его составляющих, на движение вдоль оси и на движение вдоль оси . Пусть абсолютные величины скоростей шара вдоль осей и будут и . Обозначим время обращения шара по замкнутой траектории через . Очевидно, должны выполняться следующие равенства

,

,

где – длины сторон прямоугольника, и числа вершин траектории соответственно на сторонах и .

Разделив второе равенство на первое, получим:

.

Отношение есть тангенс угла наклона звена траектории к стороне прямоугольника . Таким образом, нами снова получено установленное выше соотношение:

.

Покажем, что условие замыкания бильярдной траектории в прямоугольнике можно выразить в форме, аналогичной (1).

Заметим, что величина есть время, в течение которого шар проходит расстояние вдоль оси , равное. Аналогично, есть время, за которое шар проходит расстояние, равное, вдоль оси . Назовём и периодами движения шара соответственно вдоль осей и . Вследствие независимости движений вдоль осей и период обращения шара по замкнутой траектории связан с периодами и соотношениями: , где и – числа вершин траектории соответственно на сторонах и прямоугольника.

Введём также частоты и для движений бильярдного шара вдоль осей и: , .

Очевидно, условие замкнутости бильярдной траектории в прямоугольнике равнозначно следующему:

.

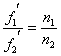Последнее соотношение по форме совпадает с соотношением для частот двух колебаний, при которых траектория частицы в колебательном процессе замыкается.

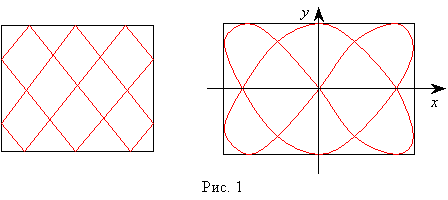
На рис. 1 для сравнения приводятся замкнутая бильярдная траектория с и и замкнутая траектория частицы, участвующей в двух колебаниях с отношением частот .

Отметим зависимость “частот” и замкнутой бильярдной траектории от угла наклона φ звена траектории к стороне прямоугольника : , . Отношение ”частот” и не зависит от величины скорости бильярдного шара.