OPTICS
Rena J. Kasumova
Baku State
University, Azerbaijan, Baku
Redoubling of optical frequency in CGA
and ZGP
The CGA and ZGP crystals present a
great interest for application in nonlinear optical frequncy converters of
laser radiation of İR-range [1-2]. The most efficient way of frequency
conversion is performed by using generation of second harmonic. It is explained
by high nonlinearity of second order in crystals –converters in comparison with
nonlinearity of the third and etc. orders.
Creation of
frequency converters with tuneable frequency of radiation is one of the actual
tasks of nonlinear optics. It is, in particular important for IR –range of
spectrum where two windows of atmosphere transparency exist. There are a number
of the perspective crystals transparent in the IR –range of spectrum. These are
CdGeAs2 (CGA), AgGaSe2, AgGaS2, ZnGeP2
(ZGP), AgGaxIn1-xSe2 and others [3-5]. But a
basic drawback of the listed crystals was their considerable absorption, worse
thermal properties what restricts an efficiency of frequency conversion in
these crystals. However, owing to the achievements of modern technology of
crystal growth, it became possible to create crystals with the improved optical
characteristics.
The
researches in this direction are being continued. It is possible to study
nonlinear interaction of optical waves by the direct numerous account of
related equations. However, development of the analytical method permits to
receive the concrete analytical expressions and determine the optimum
parameters of the task for the purpose of obtaining maximum efficiency of
conversion.
The present
work considers an efficiency of frequency conversion in CGA and ZGP crystals.
An analysis has been made in the constant –intensity approximation [6-7]
enabling to take into account the reverse influence of excited wave on exciting
one. There has been made comparison of the obtained results with the
experimental ones.
The task is
solved with the use of the well –known system of the reduced equations with
corresponding boundary conditions reflecting the process of second harmonic
generation [8-10]. In Figs. 1 and 2 the numerical solution of analytical
expressions received in the constant –intensity approximation in experimentally
realized conditions for case of CGA and ZGP crystals is shown.
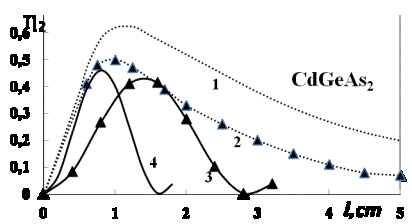
Fig. 1. Dependences of conversion efficiency of radiation
energy of pump wave (l=9.55 mcm) to
energy of wave of second harmonic h2 on lengths
of CGA crystal l calculated in the constant-intensity approximation (curves 3 and
4) and accurate counting (dotted curves 1 and 2) for d1,2=0.05 cm-1
[2], D=0,0028 cm-1
and pump intensity of I10= 30 MW/cm2 [6] (curves 2 and 3)
and 160 MW/cm2 [6] (curves 1 and 4).
In Fig. 1
dependences of frequency conversion efficiency in CGA on crystal length ![]() are displayed. There
were considered 2 versions of conversion differing by pump intensity of CO2
laser radiating on wavelength in 9.55 mcm: 30 MW/cm2 (curve 3) and
160 MW/cm2 (curve 4). It follows from behavior of curves that there
exists an expressed maximum, i.e. the optimum value of crystal length at which
conversion efficiency is maximum. As far as pump intensity increases the
maximum conversion is reached at lesser lengths of crystal, i.e. with an
increase in pump intensity the coherent length of crystal decreases. Just here
for comparison of the corresponding dependences
are displayed. There
were considered 2 versions of conversion differing by pump intensity of CO2
laser radiating on wavelength in 9.55 mcm: 30 MW/cm2 (curve 3) and
160 MW/cm2 (curve 4). It follows from behavior of curves that there
exists an expressed maximum, i.e. the optimum value of crystal length at which
conversion efficiency is maximum. As far as pump intensity increases the
maximum conversion is reached at lesser lengths of crystal, i.e. with an
increase in pump intensity the coherent length of crystal decreases. Just here
for comparison of the corresponding dependences ![]() received at the
numerical account for the system of reduced equation in relative units [2].
received at the
numerical account for the system of reduced equation in relative units [2].
In Fig.2
there are cited the analogous dependences calculated in CIA (curves 3 and 4)
and obtained experimentally [2] (curves 1 and 2) in case of conversion in ZGP
crystal. With this an examination was carried out for two values of pump
intensity: crystal breakdown value in ZGP (intensity of optical breakdown is
equal to 142 MW/cm2 [2, 11] (curves 1 and 4) and for ![]() MW/cm2 (curves 2 and 3).
MW/cm2 (curves 2 and 3).
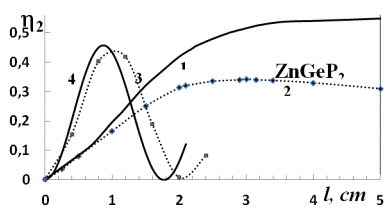
Fig. 2.
Dependences of conversion efficiency of radiation energy of pump wave (l=9.55 mcm) to energy of wave of second harmonic h2 on lengths of ZGP crystal l calculated
in the constant-intensity approximation (curves 3 and 4) and accurate counting
(curves 1 and 2) for d1,2=0.05 cm-1
[2], D=0,00065 cm-1
and pump intensity of I10= 30 MW/cm2 [6] (dotted curves 2
and 3) and 160 MW/cm2 [6] (solid curves 1 and 4).
From comparison of cited dependences it follows that
qualitative behavior of curves received in the constant –intensity
approximation and by the direct accurate calculation, coincides.
Dependences
in Fig.1 have the pronounced maxima with similar values of the optimum length
for CGA crystal calculated in the given approximation and at the precise
account. In case of ZGP crystal (Fig.2) the values of coherent lengths for two
versions of the account are differed several times. This fact may be explained
by the lack of detailed information on conditions of the experimental
researches, spread of different parameters values of the task what was also
noted by the authors [11].
The advantage
of the analytical method of research consists in that it is possible to
calculate the optimum parameters of conversion proceeding from the dimensions
of the concrete crystals –converters. And namely at the given values of crystal
–converter length it is possible to calculate an optimum value of pump
intensity, as well as to calculate the coherent length of a crystal –converter
at chosen pump intensity of laser radiator. The analytical method permits also
to estimate expected conversion efficiency at different wavelengths of laser
radiation.
References
1. K.L.
Vodopyanov, G.M.H. Knippels, A.F.G. van der Meer, J.P. Maffetone, I. Zwieback.
Opt. Commun., 202 (2002) 205-208.
2. P. P. Geiko. Atmospheric and Oceanic Optics, 16 (2003) 828-834.
3. P.G.
Schunemann, S.D. Setzler, T.M. Pollak, A.J. Ptak, T.H. Myers. J. Cryst. Growth,
225 (2-4), (2001) 440-444.
4. Yu. M. Andreev, I. S. Baturin, P. P. Geiko, and A. I.
Gusamov. Quantum Electronics, 29
(1999) 66-70.
5. S. Das. Quantum Electronics, 42 (2012) 228-230.
6. Z.H.Tagiev,
and A.S.Chirkin. Zh. Eksp. Teor. Fiz., 73
(1977) 1271-1282.
7. Z.H. Tagiev,
R.J. Kasumova, R.A. Salmanova, N.V. Kerimova. J. Opt. B: Quantum Semiclas. Opt.
3, (2001), 84-87.
8. S.A.
Akhmanov, R.V.Khokhlov, The Problems of Nonlinear Optics (Moscow, VINITI) 1964.
9. N.
Blombergen, Nonlinear Optics, W.A. Benjamin, New York, 1965.
10. V.G. Dmitriev and L.V.
Tarasov, Applied Nonlinear Optics. (Moscow, Radio I Svyaz) 1982.
11. Yu.M. Andreev, V.V. Badikov, V.G. Voevodin, L.G. Geiko, P.P. Geiko, M.V.
Ivashenko, A.I. Karapuzikov, and I.V. Sherstov, 31 (2001) 1075-1078.