Технические науки

Д.т.н. А.И. Айнабеков, д.т.н. У.С. Сулейменов, ст.преп. Л.З. Жолшиева, магистрант Г.А. Айдашева

ЮКГУ им. М. Ауезова, г. Шымкент

Расчет поврежденности конструкционных материалов при повторно-переменных нагрузках с учетом влияния температуры

Отдельные детали машин и механизмов работают в условиях высоких температур, что существенно влияет на их долговечность. В работе представляется методика инженерного расчета поврежденности по механическим свойствам стали при повторно-переменных нагрузках с учетом влияния температуры.

Опыты на малоцикловую усталость при повышенных температурах показали необходимость учета частотно-временных факторов, что было сделано в работе [1] в виде:

или

, (1)

где - частота, цикл/мин, - время до разрушения, - константа, зависящая только от температуры.

Опираясь на уравнение (1) , в работе [2] предложена зависимость вида

. (2)

Последующие исследования привели к необходимости непосредственного учета не только циклического, но и статического повреждения в цикле, установлению закономерностей поциклового накопления и суммирования статического и циклического повреждений.

Известны уравнения простого суммирования в виде:

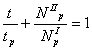, (3)

где - время накопления статического повреждения, - время до разрушения, возникающего только от статического повреждения, - число циклов до разрушения при испытании с циклами заданной длительности, - число циклов до разрушения при испытании с циклами пилообразной формы.

В работах [3,4] было показано, что правильнее суммировать доли повреждения при изотермическом малоцикловом нагружении по степенному закону

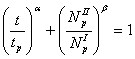, (4)

который можно выразить в циклах следующим образом:

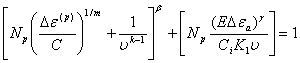, (5)

где и – постоянные кривой малоцикловой усталости по Коффину, и - постоянные кривой длительной прочности, - постоянные, зависящие от материала и температуры испытания, - коэффициент приведения цикла.

В предыдущих расчетных уравнениях циклы разной длительности (с разными выдержками при максимальной температуре) создают различную статическую повреждаемость. Однако при разделении общей повреждаемости на циклическую и статическую (3) и (5) учет частоты нагружения в этом смысле уже не является необходимым. В связи с этим часто отдают преимущество деформационно-кинетическому уравнению. Этот подход получил дальнейшее развитие в работах [5], где наиболее полно учитывается влияние временного эффекта. Согласно этой работы,

. (6)

Данные экспериментальной проверки уравнения (6) показали, что разброс накопленного суммарного повреждения - для всех рассмотренных режимов нагружения находится в пределах 0,5 – 1,5. При неизотермических условиях критериальное уравнение может быть записано в виде [6]:

, (7)

где определяется из кривой усталости с учетом времени деформирования и формы цикла нагрева, - односторонне накопленная деформация в момент разрушения, - располагаемая пластичность при монотонном нагружении в неизотермических условиях.

Вышеуказанные уравнения не позволяют дать достаточной оценки поврежденности, в связи с чем предлагается следующее кинетическое уравнение повреждений:

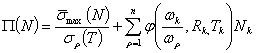(8)

Здесь: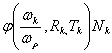- функциональный параметр, определяемый из кривых усталости при линейном напряженном состоянии в условиях разных температур и коэффициентов ассиметрии, - расчетное значение максимального главного напряжения, которое определяется в зависимости от вида напряженного состояния из условия постоянства объема, - истинное сопротивление статического разрыва. Графики функции для стали 12Х18Н10Т приведены на рисунке 1.

Влияние температуры на второе слагаемое уравнения (8) не носит наследственного характера. Поэтому, разбивая график изменения температуры во времени на небольшие ступени, мы можем вычислить пластические деформации на каждой ступени в отдельности. При этом общая поврежденность будет равна сумме поврежденностей на отдельных температурных ступенях.

По результатам проведенных расчетов на термомеханическое нагружение, приведенных в таблице 1, один температурный период отвечал приблизительно 310 циклам механического нагружения, то есть на каждом цикле механического нагружения T = const. Из кривых малоцикловой усталости при разных постоянных температурах определялись соответствующие выражения функции . Эти функции аппроксимируются степенной зависимостью вида:

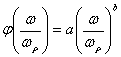, (9)

гдеи - коэффициенты, определяемые по методу наименьших квадратов.

Выражение функции при термомеханическом нагружении включает переменные коэффициенты, зависящие от числа циклов. В общем виде имеем:

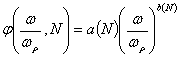. (10)

Из опытов на растяжение при разных постоянных температурах получаем зависимости и , которые для удобства расчета также выразим через число циклов N. Аппроксимирующие кривые описываются уравнениями вида:

= 380-300sin((N-1) /310);

= 1000-500sin((N-1) /310). (11)

Таким образом, усталостная поврежденность, накапливающаяся в материале при термомеханическом нагружении, определяется в виде суммы:

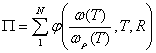(12)

Окончательно полную меру повреждений представим в виде:

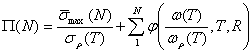(13)

Методика проведения расчета и соответствующая запись петель соответствовала ГОСТу-25.505-85. Параметры модели определялись из опытов на циклическое растяжение-сжатие и из статических диаграмм деформирования. Влияние температуры на эти параметры описывается зависимостями (10) и (11).

Результаты расчета поврежденности, произведенные по формуле (13) приведены в таблице 1.

Таблица 1

Результаты расчетов при сложном термомеханическом нагружении

для стали 12Х18Н10Т

№ опыта	, МПа R= -1	, МПа R= -1	T(N), К	, МПа	, цикл	Поврежденность по (13)
1	209	161	293-673	348	156	0,600	0,268	0,868
2	190	147	293-673	320	462	0,542	0,422	0,964
3	190	147	293-673	320	493	0,520	0,446	0,966
4	183	141	293-673	300	866	0,388	0,492	0,880
5	198	152	293-673	330	340	0,336	0,496	0,832
6	211	162	293-673	351	143	0,608	0,246	0,854

Расчетные повреждения при термомеханическом нагружении в основном получились меньше единицы, причем наибольшее расхождение достигло 22% от 1. Это расхождение можно объяснить тем, что функция в уравнении (13) определялась из испытаний образцов (рисунок 2) при заданных истинных напряжениях.

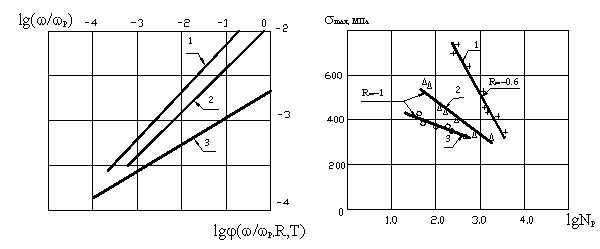
Рисунок 1. Графики функци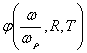и Рисунок 2. Кривые малоцикловой усталости

1,2 – при R = - 1,0, 3 – при R = -0,6 1,2 - при Т = - 273К, 3 - при Т = 673К

Полученные результаты расчетов для условий термомеханического нагружения удовлетворительно согласуются с данными испытаний. Отсюда следует, что кинетическое уравнение (13) вполне приемлемо для расчета повреждений в общем случае термомеханического нагружения конструкционных материалов, если только отсутствуют деформации высокотемпературной ползучести.

Литература:

1. Eckel J.F. The inf luence of freguency on the repeated bending life of acid // Proc. Am. Soc. Mater.-1951.- Vol.51.-P.745-756.

2. Coffin L.F. A note on low-cycle fatigue laws // J. Mater.- 1971.-Vol. 6.- P.388-402.

3. Wood D. The effect of creep on the hign strain fatigue behaviour // Welding Journal .-1966.-Vol.45, N2.-P.92-96.

4. Екобори Т., Инхикава М. Подход к проблеме взаимодействия усталости и ползучести // Сборник Механика деформируемых тел и конструкций – М.: Машиностроение, 1975. - С. 178-182.

5. Шнейдерович Р.М., Гусенков А.П. Деформационно-кинетические критерии длительной циклической прочности // Сборник Исследование малоцикловой прочности при высоких температурах.–М.: Наука, 1975.-С.39-61.

6. Гусенков А.П., Казанцев А.Г. Метод исследования закономерностей деформирования и критериев разрушения при малоцикловом неизотермическом нагружении // Заводская лаборатория. -1977. – №11. - С. 1384-1392.