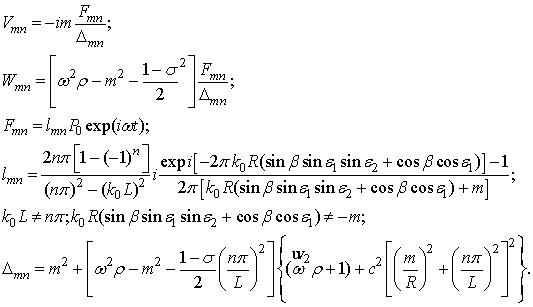Карачун В.В., Мельник В.М., Косова В.П.

Національний технічний університет України «КПІ»

ряди фур'є для визначення пружної піддатливості оболонки

Вивчення особливостей динаміки гіроскопічних приладів, що експлуатуються в умовах впливу зовнішнього аеродинамічного шуму звукової частоти, дає змогу стверджувати про тенденцію до накопичення похибки вимірів. Так, прилади орієнтирних напрямків, що не коректуються та базуються на використанні властивостей тристепеневого астатичного гіроскопа, мають систематичний дрейф осі фігури і за тривалої дії звукового випромінювання високої інтенсивності (вище за 140 децибел) можуть призвести навіть до втрати одного ступеня вільності.

Причиною цього явища є нестаціонарна пружна взаємодія підвісу гіроскопа з акустичним полем, що проявляється у вигляді додаткових збурюючих моментів інерційної природи, які виникають і обумовлені наявністю кінематичного впливу з боку основи – літального апарату.

Найбільш вразливим елементом підвісу у даному випадку виявляється кожух гіроскопа. Пружні переміщення його поверхні під дією падаючої хвилі тиску являють собою суперпозицію різних форм нелінійних коливань, що у своїй сукупності призводять до суттєвої зміни динамічного режиму приладу.

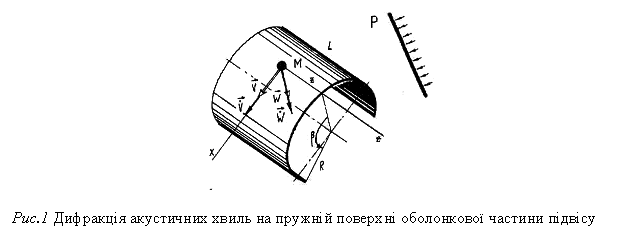
Проаналізуємо характер пружних переміщень циліндричної частини кожуха у площині шпангоута і обмежимося тільки радіальними складовими як найбільш суттєвими у кількісному та якісному вимірі.

За умови шарнірного з’єднання з торцевими поверхнями та незвичайної товщини стінок, диференціальні рівняння пружної поверхні наведемо у вигляді:

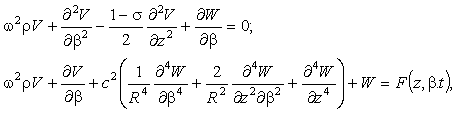(1)

де - коефіцієнт; h, R – товщина та радіус циліндричної поверхні кожуха; та - відповідно тангенціальна і радіальна складові переміщення точок бокової поверхні (рис.1); - центральний кут; L – довжина.

Граничні умови задамо у вигляді:

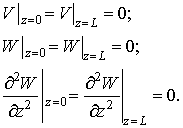(2)

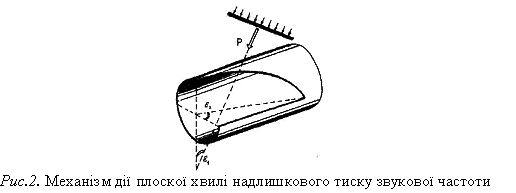
Задамо звуковий тиск у падаючій хвилі наступним чином (рис.2):

(3)

де Р₀ – тиск, що дорівнює різниці падаючої та випромінюваної поверхнею хвиль; 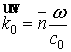- хвильовий вектор; с₀ – швидкість звуку; - одиничний вектор напрямку розповсюдження хвиль; - радіус-вектор точки простору.

Отже, приймаючи до уваги прийняті на схемі позначення, маємо:

(4)

Розв’язок системи рівнянь (1) і (2) знайдемо у вигляді рядів Фур’є функцій та у прямокутнику:

(5)

Відповідно до прийнятих граничних умов, ряд Фур’є за зміною z будується у вигляді:

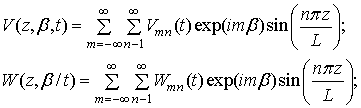(6)

де т, п – числа напівхвиль;