PhD, associate professor Mahanbetalieva Kamshat Torgaybaevna¹, master of technical sciences Tashmukhamedov Farkhad²

Tasks of the modern process of winding yarn

M.Kh Dulaty Taraz State University, Kazakhstan

The process of winding the textile yarn on a package at the body in the form of rotation involves in two interrelated processes: the process of winding yarn with a spinning (torsion) and packing process of filament coiled winding on a package at (coils, coil bobbin tubular space, spool, etc ).

In order to increase the quality of the winding becomes very essential question, related to the creation of new specialized equipment, to form a winding packing with predetermined properties.

Work in this area started at the beginning last century, was continued a number of domestic and foreign authors. Initially, the greatest contribution to the development of the theory of winding yarn on the package made by the scientists spinners as N.A. Vasiliev, I.I. Babarykov, S.S Kovner, V.A. Voroshilov, E.I Krzhyzhanovski, U.I Vinogradov and others. This was due to the fact that the roving, spinning and twisting machines required to ensure that the speed of winding yarn or twine is strictly equal to the rate of release of the product from the drafting system. In addition it was necessary to get a package at a certain shape and structure ( for example, roving coil ends, must be chamfered and closeness parallel winding, winding from the spinning machine must be carried out on a cone, moving upward as winding cop).

In all the above works was identified traverse motions (dots layout- carriage ring rail) and winding point ( points of crowding or entry point into a package). At the end of circumstances led to errors in the design of winding mechanism and unsatisfactory of quality winding roving, spinning and torsion package irregular shape coiling and ears, lack of equilibrium winding etc.

First remark was mismatch movements of crowding yarn points on the package did I.S. Myasnikov. In this work, devoted to the study of winding yarn on a spinning machine batch, it is noted that the thread during winding is tangential to the helix, and not normal to the axis of the spindle. We conclude, that the scale of the movements must be greater that the height of the cone winding, from the point moves along the winding bobbins not like the layout point. Then I.S Myasnikov with certainly notes that as a result of mismatched point motion and winding yarn guide eyelet can not get end portions of packing a given structure.

In more details on this issue was investigated by G.K Moiseev [1], who used the technique of V.A. Bluer, that researched the form transitional spiral thread and bobbin winding density. Part of the equation transition coil was not found, but the dependence between the height H winding thread guide and scope H_H:

(1)

where λ- the free length of the thread between the point and the point of the winding layout;

ϑн- the speed movement of the filament in the axial direction of the packing;

ϑо - speed winding.

The theory of spinning bobbin winding mostly developed by A.F.Proshkov. Exactly, he developed the theory of the work of designing mechanisms for winding roving, spinning and twisting machines based on the constancy of the speed of winding, free winding interval filaments and, the most important, the conditions of equilibrium winding obtained by prof. A.P. Minakov [2].

A.F. Proshkov derived a general equation in differential form if winding [3].

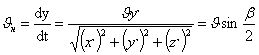(2)

where ϑн - the velocity of the wire in clash of the body winding;

x;y;z- coordinate of the point on the yarn package at crowding (where the y axis is directed along the rotation packing);

β - crossing wind turns.

Using the above formula, A.F. Proshkov determined that regularity can move the winding, pitch wind and pitch of axis package of various shapes.

Professor A.P. Minakov gave conditions for obtaining equilibrium winding in which the coils do not fall from the surface of the packing it is wound. The first (and main) condition for the equilibrium is winding forms on the surface coil winding, it has the form:

tgӨ≤ μ (3)

where Ө- geodesic deviation winding turn;

μ- the coefficient of fiction the surface coil winding.

Geodesic deviation winding depends mainly in crossing turns and taper winding of packing.

(4)

where R- radius of the winding current packing;

β- current crossing wind turn;

At the constant rates of the yarn guide and the corner velocity of rotation of the packing:

(5)

where -the taper angle of packing.

Condition thread tension

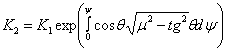, (6)

where K₁ and K₂- vanishing tension and turn upwind branches;

ψ – the angle of coil winding.

Using theoretical developments of G.K.Moiseev and A.P.Minakov, professor A.F.Proshkov decided a number of issues in designing winding mechanisms for optimal bobbins shape and structure (packages with the faces of a predetermined shape and having a stable equilibrium). However, of the fundamental equation winding he made some inaccuracy, assuming that the point of winding all the time moves on forming the package. This inaccuracy noticed E.D. Efremov and to eliminate the mistakes brought the so- called kinematic equations winding [4], some are as follows:

(7)

where γ – the corner between the perpendicular dropped from the point of winding axle oz, and the plane xoy;

- length of the perpendicular from the point of pickup to the axis of rotation of packing oz;

X and Y – coordinates of the current layout – the corner between perpendicular, dropped from a point on the layout axis OZ, and the XOY plane;

ƒ= R +(Z- z)R’ – auxiliary function.

R- current winding radius of packing, depends on z;

Z- current applicate point layout;

z- winding current applicate point;

ω- angular speed of the pakage.

Thus, from the A.F. Proshkov, E.D. Efremov the axis of rotation of the packing took no axis OY , and the axis OZ of the first equation, and its practically introduced the concept of the line winding on which entry point and moves winding filament. Obviously, if γ-const for the entire course of the movement of the yarn guide, the line coincides with the generator winding packing.

Kinematic equation of the coordinates of points tied winding layout and crowding. Calculations, carried out by the formulas E.D. Efraim (eg speed winding yarn on the package, the crossing angle turns, etc.) give more accurate results ( 2-3% different from the results obtained from the formulas of A.F. Proshkov).

Using the kinematic equation winding , E.D. Efremov found a more general solution made by G.S. Janitor, V.A. Blyuer and A.F.Proshkov on the definition of the laws of winding yarn on the package after the sudden stop of the yarn guide.

All these major theoretical developments undertaken by N.A. Vasiliev,

I.S. Myasnikov, V.A. Blyuer, G.K. Moiseev, A.P. Minakov, A.F. Proshkov, E.D.Efremov and others aimed at finding ways to stabilize the winding speed, obtaining optimal (not heavily compacted and beveled)ends packages and creating equilibrium coils. However, the establishing of high- speed textile production of crossmotal machines has set theorists winding yarn, a number of new tasks that require their immediate solutions. First, the wounding on different spools these machines lack a specific density of winding, uneven and f importantly in axial and radial direction of the package.

Secondly, there was sever abrasion of the wound yarn drum, resulting in loss of its strength properties.

Thirdly, under certain winding diameter disrupted by dispersion of surface coils, and the packing was observed the formation of bundles.

Fourth, in some cases, there were rallies turns on the ends of the wound bobbin.

Fifthly, there is squeezing turns on the ends of the spool and the corrugations formed.

Literature:

1. Moiseev G.K. Investigation of cross- wound on a cylindrical bobbin on continuous production process of viscose fiber. Ph.D., Dissertation St. Peterburg. 1958.

2. Minakov A.P. Basis of the theory of winding and unwinding of the thread. M//Textile industry.- 1994.№ 10.s11. №11-12 p 10.

3. Proshkov A.F. Investigation of the processes associated with the filament winding and winding design mechanisms. D.t.s. Dissertation. M. 1965.

4. Efremov E.D Basics of the theory of winding yarn on the package.M.Legpisheprom. 1982.

5. Pannin I.V. Development and research of textile structures packages for special purposes. Ph.D., Dissertation. M. 1996.