доктор PhD, преподаватель Ишуова Ж.Ш.

Казахский Национальный Университет имени аль–Фараби, Казахстан

Линеаризация соотношений ДСОР модели и ее решение с помощью метода Бланшара–Кана

В рассматриваемой модели имеются две незаданные переменные ỹ_t+1 и π_t+1. Согласно работе О. Бланшара и Ч. Кана [1], система разностных уравнений будет иметь единственное равновесие, если и только если оба собственных значения матрицы A_T размерности 2х2 находятся внутри единичной окружности. Рассмотрим рекурсивную систему вида X_t=AE_t{X_t+1}+ε_t^X, где X_t – это вектор заданных и незаданных переменных, а ε_t^X – вектор экзогенных переменных. О. Бланшар и Ч. Кан [1] доказали, что существует единственное равновесие, если и только если число собственных значений матрицы A внутри единичной окружности равно числу неопределенных переменных. Бесконечное же число равновесий существует, если число собственных значений внутри единичной окружности будет меньше, чем количество незаданных переменных. Если число собственных значений внутри единичной окружности превышает количество незаданных переменных, то равновесие существовать не может. Охарактеризуем необходимые и достаточные условия для этого свойства. Два собственных значения, обозначенные Λ₁ и Λ₂, как правило, являются решениями следующей системы, записанные в матричном виде, где I представляет собой единичную матрицу│A_T–ΛI│=0. В нашем случае система будет выглядеть следующим образом:

.

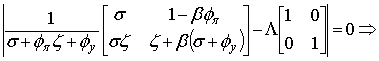
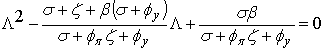Дж. Ласалле [2] доказал, что корни квадратного уравнения x²+a₁x+a₀=0 будут меньше единицы, если и только если │a₀│<1, а │a₁│<1+a₀. Следуя работе Дж. Ласалле [2], мы знаем, что два собственных значения матрицы A_T находятся внутри единичной окружности, если и только если выполняются следующие два неравенства:

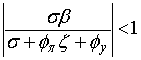и .

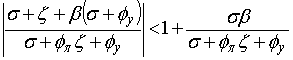Параметры экономической политики ϕ_y и ϕ_π должны удовлетворять этим двум неравенствам. Из первого неравенства следует:

σ(β–1)<ϕπζ+ϕy

(1)

Очевидно, что условие (1) и, следовательно, первое неравенство, должны выполняться при β<1. Таким образом, единственное соответствующее неравенство – это второе неравенство, которое мы перепишем в виде:

ζ(ϕπ–1)+(1–β)ϕy>0

(2)

Мы видим, из условия (2), что равновесие однозначно определяемо до тех пор, пока параметры денежно–кредитной политики имеют довольно высокие значения, т.е. до тех пор, пока монетарные власти реагируют на отклонения инфляции и выпуска с достаточной силой. Также отметим, что требование, предъявляемое к параметру ϕ_π>1, является достаточным условием для неравенства (2). Это условие называется принципом Тейлора. Предположим, что экономика подвержена постоянным изменениям уровня инфляции равным dπ. Из формулы новой кейнсианской кривой Филлипса π_t=βE_tπ_t+1+ζỹ_t ясно, что без применения мер денежно–кредитной политики, изменение уровня инфляции приведет к отклонению разрыва выпуска на величину равную dỹ=[(1–β)/ζ]dπ.

Однако с учетом правил денежно–кредитной политики, мы можем определить реакцию номинальной процентной ставки, вставив соотношение dỹ=[(1–β)/ζ]dπ в правило процентной ставки (2.63), установленное Тейлором:

.

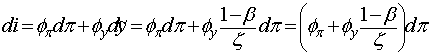Кроме того, путем перестановки параметров в неравенстве (2) получаем, что . Следовательно, изменения в уровне инфляции должны покрываться за счет больших изменений в номинальной процентной ставке. Как следствие это будет стимулировать повышение реальной процентной ставки, и выступать в качестве стабилизирующей силы. Таким образом, из условия (2) видно, что, когда центральный банк достаточно агрессивно реагирует на изменения в уровне инфляции и разрыве выпуска, то есть когда значения параметров ϕ_π и ϕ_y достаточно велики, объем производства вынужден вернуться к своему естественному уровню, а инфляция обратно к нулю.

Искажения эффективного распределения. Эффективное устойчивое состояние. В своей работе Р. Франк [3, с. 615–616] приходит к выводу, что базовой моделью общего равновесия является рыночная модель, состоящая из двух потребителей и производителей. Если представить, что изначально каждому потребителю распределили одинаковое количество товаров, то рыночный обмен, в конечном счете, все равно истощит возможные взаимные выгоды от торговли. Такой результат известен под названием теоремы о «невидимой руке» или об экономике благосостояния. При выпуклой кривой безразличия, эффективное распределение рассматривается в качестве конкурентного равновесия. Это доказательство в свое время было названо второй теоремой экономики благосостояния. Смысл этой теоремы состоит в том, что она описывает различие между проблемой эффективности и равновесного распределения. Потребители и производители изначально могут распределить имеющиеся блага исходя из принципа справедливости, а уже потом использовать рынки в качестве площадки для гарантирования эффективного использования имеющихся благ.

Литература:

1. Blanchard O.J, Kahn C.M. The solution of linear difference models under rational expectations // Econometrica. – 1980. – Vol. 48, №5. – P. 1305–1312.

2. LaSalle J.P. The stability and control of discrete processes. – New York etc., Springer–Verlag, 1986. – 150 p.

3. Франк Р.Х. Микроэкономика и поведение. – М.: Инфра–М, 2000. – 696 с.