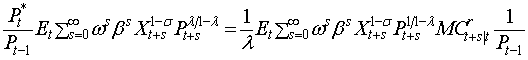доктор PhD, преподаватель Ишуова Ж.Ш.

Казахский Национальный Университет имени аль–Фараби, Казахстан

Лог–линеаризация формулы оптимальной цены около устойчивого состояния в ДСОР моделях

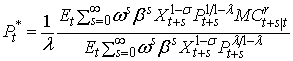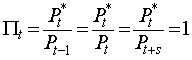Следующий шаг заключается в лог–линеаризации около устойчивого состояния формулы оптимальной цены . В устойчивом состоянии, определяемой нулевой инфляцией, получаем: , Y_t+s│t=Y_t│t, I_t,t+s=β^s, .

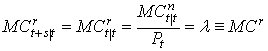Последние три тождества вытекают из определения о нулевой инфляции и рыночном равновесии. Перед тем как лог–линеаризировать дробное выражение для оптимальной цены P_t^*, целесообразно разделить обе части рассматриваемой формулы оптимальной цены на P_t–1: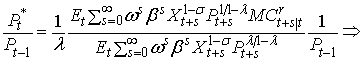

(1)

Проведем преобразование левой части уравнения (1) в ряд Тейлора первого порядка. Первое слагаемое в левой части (1) находится в стационарном состоянии. Четыре последних слагаемых содержат первые производные по P_t^*, P_t–1, P_t+s и X_t+s соответственно. Все переменные оценены в устойчивом состоянии:

.

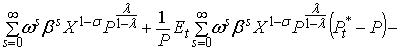
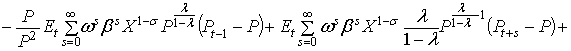
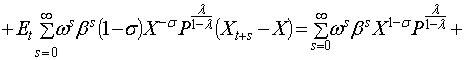
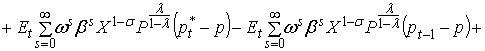
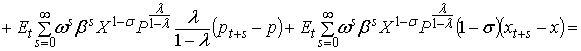
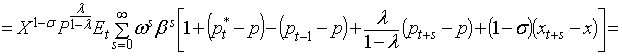
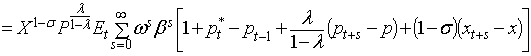Разложение в ряд Тейлора первого порядка правой части уравнения (1) выглядит следующим образом: первое слагаемое в правой части (1) находится в стационарном состоянии. Четыре последних слагаемых содержат первые производные по P_t–1, P_t+s и X_t+s и соответственно. Все переменные оценены в устойчивом состоянии:

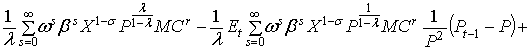
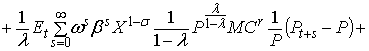
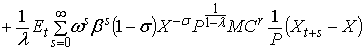
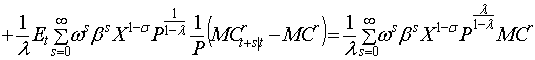
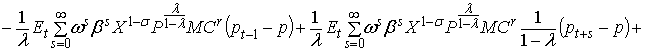
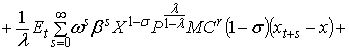
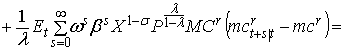
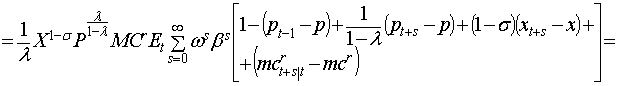
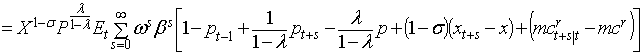В заключении приравняем левую и правую часть уравнения (1) тем самым определив оптимальную цену :

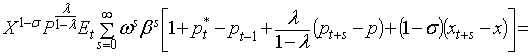
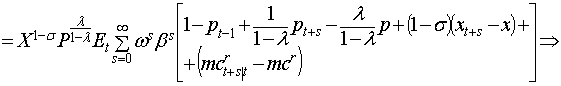
. Так как есть бесконечно убывающая геометрическая прогрессия, у которой и первый член и знаменатель равен произведению ωβ, следовательно .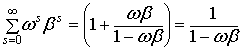

.
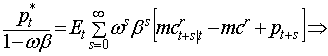
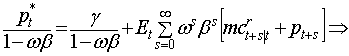