доктор PhD, преподаватель Ишуова Ж.Ш.

Казахский Национальный Университет имени аль–Фараби, Казахстан

Влияние шоков денежно–кредитной политики

Один из методов для определения такого влияние – это метод неопределенных коэффициентов. Начнем, сделав следующие допущения:

ỹt=χyυt	(1)
πt=χπυt	(2)

где коэффициенты χ_y и χ_π еще предстоит определить. Для начала подставим следующие условия (1) и (2) в формулу новой кейнсианской кривой Филлипса и найдем выражение для параметра χ_yυ:

π_t=βE_tπ_t+1+ζỹ_t

χ_πυ_t=βχ_πρ_υυ_t+ζχ_yυ_t

(1–βρ_υ)χ_π=ζχ_y

(3)

Затем вставим правило процентной ставки, установленное Тейлором в формулу динамической кривой IS. Чтобы сделать анализ как можно более прозрачным введем предположение, что , т.е. в модели не будет проанализировано влияние технологических шоков.

.

Определим коэффициент χ_π используя формулы (1)–(3):

(4)

Если теперь подставим (4) в (3), то получим формулу для коэффициента χ_y:

(5)

Используя формулы для неопределенных коэффициентов (4) и (5) в условиях для разрыва выпуска (1) и, соответственно инфляции (2), получаем новый вид ранее установленных предположений:

ỹt=–(1–βρυ)Χυυt

(6)

πt=–ζΧυυt

(7)

где .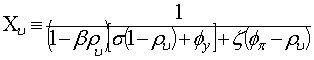

Если условие 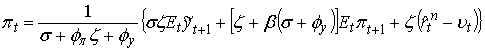выполняется, то коэффициент Λ_υ будет больше нуля. Заметим также, что если подставить авторегрессионный процесс первого порядка в дважды модифицированные уравнения динамической кривой IS (6) и в новую кейнсианскую кривую Филлипса (7), то получим следующие соотношения:

.

Таким образом, экзогенное увеличение процентной ставки приводит к устойчивому снижению разрыва выпуска и инфляции. Так как естественный уровень выпуска не зависит от шока денежно–кредитной политики, то реакция объема производства совпадает с разрывом выпуска. Кроме того, динамическая кривая IS и ее модифицированная версия (1) могут быть использованы для получения отклонения реальной процентной ставки от своего устойчивого состояния, тогда девиация естественной реальной ставки процента будет выглядеть как:

(8)

Отклик на номинальную процентную ставку сочетает в себе прямое влияние υ_t и косвенное влияние индуцированного сокращенного разрыва выпуска и инфляции. Из уравнений (7) и (8) получаем выражение для отклонения номинальной процентной ставки:

(9)

Заметим, что если шок денежно–кредитной политики ρ_υ является достаточно высоким, то номинальная процентная ставка начнет снижаться в ответ на рост υ_t. В этом случае, несмотря на более низкую номинальную процентную ставку, шок денежно–кредитной политики по-прежнему будет отрицательно воздействовать на выпуск, поскольку объем производства находится в обратной зависимости от реальной процентной ставки, которая однозначно поднимется через некоторое время. Наконец для осуществления желаемого изменения в процентной ставке необходимо определить изменение количества денег в обращении, используя уравнение спроса на деньги и условие совокупного рыночного равновесия:

m_t=p_t+y_t–ηi_t куда мы вставляем новую кейнсианскую кривую Филлипса (7), уравнение динамической кривой IS (6) и выражение для отклонения номинальной процентной ставки (9):

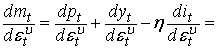
(10)