ОЦЕНКА ЭФФЕКТИВНОСТИ МОДИФИЦИРУЮЩИХ ДОБАВОК

ВЕРОЯТНОСТНЫМИ МЕТОДАМИ

Маркелова А.О., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

Рассмотрим приложение вероятностных методов оценке эффективности применения некоторой добавки в композиционном материале. Пусть А - событие, заключающееся в использовании добавки; В - факт получения необходимых свойств. Тогда - вероятность получения необходимых свойств при использовании данной добавки, - вероятность получения указанных свойств без применения добавки. Знания этих двух вероятностей вполне достаточно для суждения об эффективности добавки. Вероятность даёт представление о том, насколько возможно получить необходимые свойства добавлением этой компоненты. Но, не зная о степени невозможности получить указанные свойства без применения данной компоненты (), нельзя судить о степени целесообразности применения добавки. Поскольку применение добавки субъективно, то при характеристике зависимости между A и B с помощью одного коэффициента его следует выбрать так, чтобы он не изменял своего значения при изменении P (AB) при неизмененых значениях и .

Отметим, что нельзя вполне охарактеризовать зависимость между событиями при помощи одного числа. Для полной характеристики надо знать 3 числа, которые позволили бы определить вероятности всех 4 совмещений: AB, , (их сумма, как вероятность суммы единственно возможных несовместных событий, равна 1; для независимых событий , а для зависимых: ). Связь между событиями B и A , в известной мере, характеризуется величиной , в общем случае d оказывается мало пригодной для оценки эффективности применения добавки, т.к. она существенно зависит от P (A): .

Константа (коэффициент регрессии события В относительно события А)

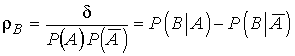
показывает, насколько увеличивается вероятность получения необходимых свойств при применении добавки; так же как и связь d, обращается в нуль тогда и только тогда, если A и B назависимы ( имеет знак d ).

Если вероятность одного факта возрастает после наступления другого, то d > 0; если наступление одного из них уменьшает вероятность другого, то d < 0

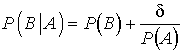(; ; , так как и положительны и меньше единицы).

Коэффициент регрессии ; .

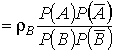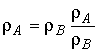Знание обоих коэффициентов позволяет, по существу, определить взаимоотношение между A и B, так как каждый из них выражает разность между вероятностями одного из событий в случае наступления или ненаступления другого.

Для характеристики зависимости между A и B иногда можно ограничиться указанием средней геометрической из обоих коэффициентов регрессии:

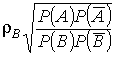
(коэффициент корреляции между A и B; знак R совпадает со знаками коэффициентов регрессии r_A и r_B).

Справедливо: ; ; R_{A B} = 0 тогда и только тогда, когда A и B независимы; , причём R = 1 тогда и только тогда, когда ; тогда и только тогда, когда ; 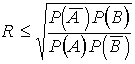, иначе была бы отрицательной. Коэффициент корреляции может быть значительно меньше 1 и, несмотря на это, А может быть следствием В; даёт весьма неточное представление о характере зависимости между А и В, если кроме R неизвестны индивидуальные вероятности этих событий (или по крайней мере значение 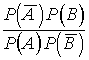, являющееся наибольшим значением R при данных P (A) и P (B) £ P (A), которое позволяет определить оба коэффициента регрессии).

Очевидна возможность использования указанных результатов для решения и обратной задачи (задача экспертизы): определить факт использования добавки при наличии определённых свойств у материала. Для большей наглядности примем: .

Имеем и существенно зависит от и , то есть от вероятности использования и неиспользования добавки (связь d плохо характеризует эффективность применения добавки). С учётом r_B = - , следует, что вероятность получения необходимых свойств при применении добавки больше вероятности получения необходимых свойств без применения добавки на r_B = 0,1. Коэффициент регрессии , но он менее интересен в рассматриваемом случае, ибо показывает, насколько вероятнее применение добавки в случае получения необходимых свойств, чем вероятность применения добавки при отсутствии необходимых свойств.

Предложенный подход эффективно использовался при синтезе композиционных материалов со специальными свойствами [2].

Литература

1. Данилов А.М., Гарькина И.А. Теория вероятностей и математическая статистика с инженерными приложениями: учебное пособие / – Пенза: ПГУАС. – 2010. – 228 с.

2. Баженов Ю.М., Гарькина И.А., Данилов А.М., Королев Е.В. Системный анализ в строительном материаловедении: монография. – М.: МГСУ: Библиотека научных разработок и проектов. – 2012. – 432 с.