ОЦЕНКА ПАРАМЕТРОВ РАБОТЫ

СТАНЦИИ ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ АВТОМОБИЛЕЙ

Свиридова М.А., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

Рассмотрим приложение теории систем массового обслуживания к организации работ на станции технического обслуживания автомобилей [1,2]. Пусть на вход системы массового обслуживания поступает простейший поток с плотностью , время обслуживания одной заявки – показательное (с параметром 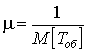). Заявка, заставшая все каналы занятыми, становится в очередь и ожидает обслуживания до ; если обслуживание до не начнется, то заявка покидает систему. Срок считается случайным и распределенным по показательному закону (плотность потока уходов заявки, стоящей в очереди) 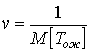. При получим систему с отказами; при - чистую систему с ожиданием. Пусть 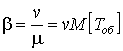. Тогда определяет среднее число уходов заявки, стоящей в очереди, приходящееся на среднее время обслуживания одной заявки. Можно показать, что

; .

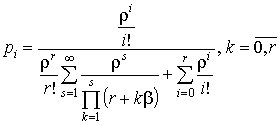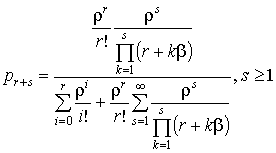Тогда среднее число заявок, находящихся в очереди, составит

.

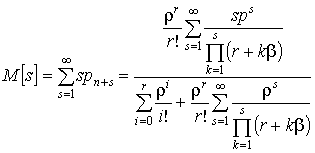Вероятность того, что заявка покинет систему необслуженной, определится в виде

.

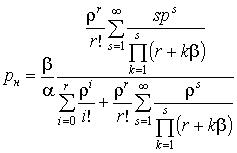Относительная пропускная способность СМО определит вероятность того, что заявка, попавшая в систему, будет обслужена . Очевидно, что пропускная способность системы с ожиданием, при тех же и , будет всегда выше, чем пропускная способность системы с отказами: в случае наличия ожидания необслуженными уходят не все заявки, заставшие каналов занятыми, а только некоторые. Пропускная способность увеличивается при увеличении среднего времени ожидания .

Для систем с ограничением по длине очереди справедливо

, ; ,.

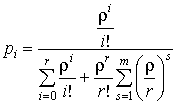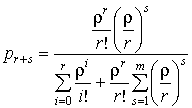Вероятность того, что заявка покинет систему необслуженной, равна вероятности того, что в очереди уже стоят заявок (число заявок в очереди ).

В системе с ожиданием в случае простейшего потока и показательного времени обслуживания имеет место случайный процесс Маркова (процесс без последействия; будущее развитие зависит только от достигнутого в момент t₀ состояния и не зависит от того, как происходило развитие в прошлом до момента t₀).

Сразу после включения системы в работу возникает переходный нестационарный процесс. После затухания переходного процесса система перейдет на стационарный установившийся режим, вероятностные характеристики которого не будут зависеть от времени (существование таких решений определяется эргодическими теоремами). Стационарные вероятности определяются из уравнений:

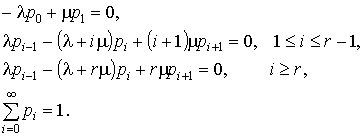
Метод прошел апробацию при проектировании станции технического обслуживания, имеющей три подъемника. Предполагалось: рабочий день продолжается 8 часов, необходимость в подъемнике возникает четыре раза, среднее время обслуживания одной заявки часа.

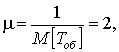
Так как (), то установившийся режим обслуживания существует. Имеем . Откуда вероятность наличия очереди равна ; средняя длина очереди .

Литература

1. Данилов А.М., Гарькина И.А. Сложные системы: идентификация, синтез, управление: монография. – Пенза: ПГУАС. – 2011. – 308 с.

2. Карев М.Н., Гарькина И.А. Вероятностные модели автотранспортных предприятий / Вестник магистратуры. – 2013. – №12. Том IV. – С.24-27.