Вишневецкий А.Л., Попов Н.С.

Харьковский национальный автомобильно-дорожный университет, Украина

Решение задачи потребительского выбора

Потребитель располагает доходом Q, за который он приобретает два продукта (если продуктов больше, часто выделяют один продукт, а вторым считают все остальные). Математическая модель поведения потребителя называется моделью потребительского выбора. Потребительский набор – это вектор (x1,x2), где координата xi  равна количеству единиц i-го продукта (i=1,2).

На множестве потребительских наборов (x1,x2) определена функция u(x1,x2) (функция полезности потребителя), значение u(x1,x2) которой на наборе (x1,x2) равно оценке потребителем этого набора.. Каждый потребитель имеет, вообще говоря, свою функцию полезности. Если набор А предпочтительнее набора В, то u(А)>u(В).

Функция полезности имеет следующие свойства:

1.     Если x>x, то u(x,x2)> u(x,x2); если x>x, то u(x1, x)> u(x1, x).

Иначе говоря, u(x1,x2)=u>0, u(x1,x2)=u>0. Производные u и u называются предельными полезностями 1-го и 2-го продуктов соответственно.

2.     Предельная полезность каждого продукта уменьшается, если объём его потребления растёт (закон убывания предельной полезности). Из свойства второй производной следует, что u(x1,x2)<0, u(x1,x2)<0.

3.     Предельная полезность каждого продукта увеличивается, если растёт количество другого продукта. Если блага могут замещать друг друга в потреблении, свойство не выполняется. u(x1,x2)=u12>0, u(x1,x2)=u21>0.

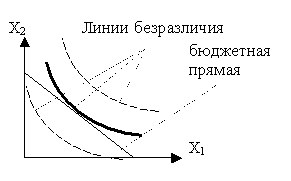
Линия уровня функции u(x1,x2) называется линией безразличия. Линии безразличия, соответствующие разным уровням удовлетворения потребностей, не пересекаются и не касаются. Чем выше и правее расположена линия безразличия, тем большему уровню удовлетворения потребностей она соответствует. Условия 1-3 означают, что функция u(x1,x2) убывает и выпукла вниз.

Задача потребительского выбора имеет вид:

u(x1,x2)→max

при ограничении  

p1x1+p2x2≤Q   ( x1≥0, x2≥0).

Допустимое множество (т.е. множество наборов продуктов, доступных для потребителя) есть треугольник, ограниченный осями координат и бюджетной прямой. На этом множестве требуется найти точку, принадлежащую кривой безразличия с максимальным уровнем полезности.

Набор (х, х), который является решением задачи потребительского выбора, принято называть оптимальным для потребителя.

Если на каком-то потребительском наборе (x1,x2) бюджетное ограничение p1x1+p2x2≤Q будет выполняться в виде строгого неравенства, то мы можем увеличить потребление какого-либо из продуктов и тем самым увеличить функцию полезности. Следовательно, набор (х, х), максимизирующий функцию полезности, должен обращать бюджетное ограничение в равенство, т.е. p1х+p2х=Q.

Итак, задачу потребительского выбора можно заменить задачей на условный экстремум (ибо решение (х, х) этих двух задач одно и то же)

u(x1,x2)→max                        

при условии  p1x1+p2x2=Q.

Для решения этой задачи применим метод Лагранжа. Для функции Лагранжа  L(x1,x2, λ)= u(x1,x2)+ λ (p1x1+p2x2-Q), получаем систему уравнений:

                                            L= u+λ p1=0,

                                              L= u +λ p2 =0,

L=p1x1+p2x2-Q =0.

Исключив из полученной системы неизвестную λ, получим систему двух уравнений с двумя неизвестными x1, и x2

                                            =,

p1x1+p2x2=Q .

Решение (х, х) этой системы есть критическая точка функции Лагранжа. Подставив решение (х, х) в левую часть равенства

=,

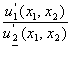получим, что в точке (х, х) отношение  предельных полезностей u(х, х) и u(х, х) продуктов равно отношению их рыночных цен p1 и p2:

=.                                                      (1)

Так как отношение равно предельной норме замены первого продукта вторым в точке локального рыночного равновесия (х, х), из (1) следует, что эта предельная норма равна отношению рыночных цен  на продукты.

Приведённый результат играет важную роль в экономической теории.

Геометрически решение (х, х) можно интерпретировать как точку касания линии безразличия функции полезности u(x1,x2) с бюджетной прямой  p1x1+p2x2=Q. Это определяется тем, что отношение =- равно тангенсу угла наклона линии уровня функции полезности, а отношение   - представля­ет собой тангенс угла наклона бюджетной прямой. Поскольку в точке потребительского выбора они равны, то в этой точке происходит касание данных двух линий.

Пример решения задачи потребительского выбора.

Оптимальный набор потребителя составляет 6 ед. продукта х1 и 8 ед. продукта х2. Определить цены потребляемых благ, если доход потребителя равен 240 грн. Функция полезности потребителя: u(x1,x2)=xx.

Решение. Получаем систему уравнений:

=,                          =,                   =,

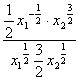p1x1+p2x2=240.                p1x1+p2x2=240 .                  p1x1+p2x2=240 .

Подставив  х1 = 6 ед.,  х2 = 8 ед., получим:  p1=10 грн., p2=22.5 грн.

 

Литература

1.      Основи вищої математики (для економічних спеціальностей): Посібник. - Львів, 2008.

2.     Красс, М.С. Основы математики и её приложения в экономическом образовании: Учебник. – 3-е изд. – М.: Дело,2002

3.     Пономаренко O.I., Перестюк M.O., Бурим B.M. Основи математичної економіки. – К.: Інформтехніка, 1995.

4.     Сборник задач и упражнений по высшей математике: мат. программирование: Учеб. Пособие/ А.В. Кузнецов, В.А. Сакович, Н.И. Холод; Под. общ. ред. А.В. Кузнецова – Мн.: Выш. шк., 2002.