Математика/5. Математическое моделирование

Канд. физ.-мат. наук Вендина А.А.

Ставропольский государственный педагогический институт, г. Ставрополь

Неявный метод оценки фрактальной размерности природных пористых систем

Общие закономерности процесса конвективно-диффузионного переноса примесей подземными водами и влияние на этот процесс макро и микродисперсии в пористых природных средах, удовлетворительным способом описываются модельным дифференциальным уравнением нелинейной миграции

, (1)

где – концентрация загрязнений подземных вод в момент времени в точке ; – скорость движения подземных вод; – активная пористость грунта; – коэффициент конвективной диффузии; – концентрация вещества в твердой фазе; – коэффициенты скорости массообмена, характеризующие условия взаимодействия вещества в твердой и жидкой фазах в статических условиях равновесия.

Из уравнения (1) следует, что профили распределения примесей существенным образом зависят от входящего в него коэффициента дисперсии , как правило, определяемого экспериментальными или статистическими методами. Коэффициент дисперсии зависит от геометрических характеристик, структуры пористой среды и свойств фильтрующейся жидкости. Основные закономерности дисперсии для различных сред в зависимости от скорости фильтрации описываются следующими [2, стр. 294] экспериментально установленными формулами:

, (2)

. (3)

Здесь коэффициент характеризует структуру и геометрию порового пространства.

Коэффициент конвективной дисперсии в том случае, когда скорость фильтрации потока велика, но закон Дарси считается справедливым, не зависит от молекулярного перемешивания и тогда для дисперсии, в силу формул (2) и (3), справедлива формула

. (4)

При незначительных скоростях фильтрации, когда , для коэффициента дисперсии принимается линейная зависимость вида

. (5)

Вывод модельных уравнений дисперсии (2) – (5) неразрывно связан с принципом локальности, согласно которому природные пористые системы рассматриваются как неоднородные с усредненными фильтрационными характеристиками для всей системы в целом. При этом, при решении многих задач прикладного характера, коэффициент дисперсии принимается постоянным, экспериментально определяемым для каждого типа почв и почвогрунтов. Однако используемый в расчетах принцип локальности во многих случаях может привести к несовпадению истинной концентрации загрязнения с прогнозной, рассчитанной по усредненным параметрам пласта. Это объясняется тем, что неоднородность порового пространства, оказывающая влияние на характер распространения миграции, вызывает ускоренное продвижение загрязненных веществ по более проницаемым поровым каналам, что приводит к нелинейным явлениям. Используемые методы расчета классической теории миграции не способны описать возникающие эффекты памяти и проникновения «языков» примесей.

Для учета нелинейных особенностей процесса миграции примесей в природных пористых системах выдвигается гипотеза о том, что параметр в модельном представлении коэффициента дисперсии (5), характеризующий структуру порового пространства и описывающий топологию внутренней структуры почв и почвогрунтов, учитывает также его фрактальные особенности, то есть – параметр, характеризующий фрактальные свойства природной пористой среды. В этом случае уравнение миграции при равномерном одномерном стационарном режиме фильтрации принимает вид

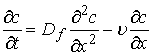, (6)

где .

Дифференциальное уравнение в частных производных параболического типа (6) является математической моделью для прогноза примесей в подземных водах. Надежность этих таких прогнозов в значительной степени зависит от достоверности кинетического параметра .

Задача определения коэффициента фрактальной дисперсии является одной из центральных проблем прогноза концентрации примесей в потоке подземных вод в природных пористых средах, которая, в случае отсутствия кинетики массообмена между веществом в твердой и жидкой фазах, сводится к решению следующей начально-краевой задачи миграции примесей.

Задача 1. Найти в прямоугольной области решение уравнения

,

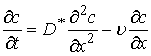удовлетворяющее условиям

, ,

, , ,

где , , – некоторые заданные постоянные величины.

Решение задачи 1 получено в виде [1] ряда

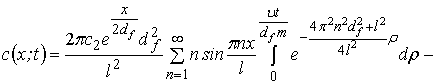
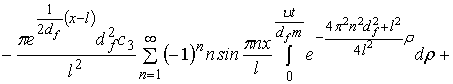
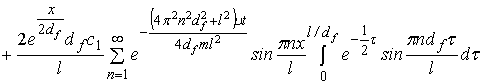. (7)

Равенство (7), вычисляя непосредственно интегралы в правой части, можно записать в виде

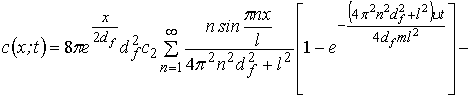
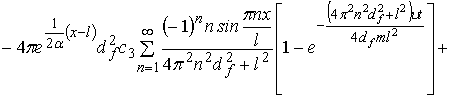
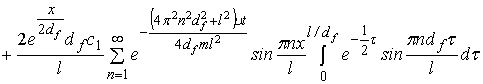. (8)

Из (8) получаем следующее асимптотическое (при ) представление функции концентрации примесей:

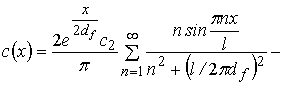
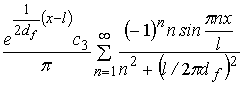. (9)

Выражение (9), учитывая известные соотношения [3, стр. 54] для сумм тригонометрических рядов

, ;

,

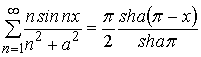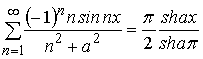представим в виде

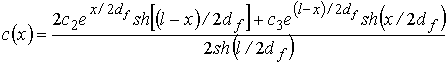. (10)

Полученное выражение (10) есть нелинейное алгебраическое уравнение относительно пространственной переменной . Оно, в случае, когда значение концентрации в произвольной точке известно, представляет нелинейное алгебраическое уравнение относительно неизвестного фрактального параметра

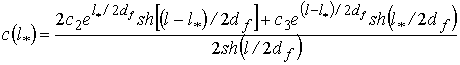. (11)

Модельное уравнение (11) представляет собой эффективный численный алгоритм расчета фрактального коэффициента дисперсии по известным характеристикам загрязнений подземных вод: расчетному слою и значению концентрации примесей в произвольной точке расчетного слоя .

Литература:

1. Веригин Н.Н. О кинетике растворения и выноса солей при фильтрации воды в грунтах // Растворение и выщелачивание горных пород. М.: Госстройиздат, 1957. С. 17–27.

2. Гавич И.К. Гидрогеодинамика. М.: Недра, 1988. 349 с.

3. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм рядов и произведений. М.: Физматгиз, 1963. 1108 с.