Рыбкин Д

Рыбкин Д.С., Хопта А.Е.

Лесосибирский педагогический институт – филиал СФУ

Применение свойств вневписанной окружности

к решению задач

“Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать”.

Г. Галилей

Решение некоторых геометрических задач и, прежде всего, задач на построение, связано с использованием понятия вневписанной окружности, которая представляется «изысканным элементом геометрии треугольника» [1: 28].

Вневписанной окружностью называется окружность, касающаяся стороны треугольника и продолжений двух других сторон.

Отметим, что для каждого треугольника существуют три вневписанные окружности, их радиусы будем обозначать r_a, r_b и r_c в зависимости от того, какой стороны треугольника они касаются.

Отметим следующие наиболее употребительные свойства вневписанной окружности.

Свойство 1. Биссектриса внутреннего угла ВАС треугольника ABC и биссектрисы двух внешних углов при вершинах В и С пересекаются в одной точке.

Доказательство. Проведем внешние биссектрисы из вершин В и С (рис. 1). Пусть они пересекаются в точке J_а. Докажем, что биссектриса угла ВАС проходит через точку J_a. Все точки биссектрисы равноудалены от сторон угла, значит, расстояния от точки J_адо прямых ВС и АС равны т.е. J_aT₁=J_aT₃,так как J_aлежит на биссектрисе угла ВСТ₁. Аналогично, равны расстояния от точки J_адо прямых ВС и АВ, т.е. J_aT₂=J_aT₃. Тогда очевидно, что точка равноудалена от прямых АС и АВ, т.е. лежит на биссектрисе угла ВАС.

Из свойства 1 следует, что существует окружность с центром в точке J_a, касающаяся прямых АС, АВ и ВС.

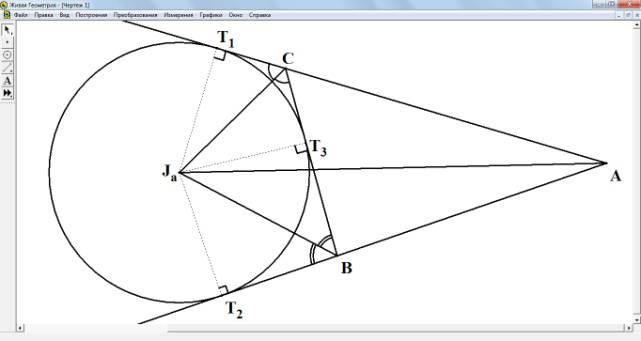
$C:\Users\Артур\Desktop\1.jpg$

Рис. 1

Свойство 2. Пусть Т₁ - точка касания вневписанной окружности с продолжением стороны АС треугольника ABC. Тогда длина отрезка АТ₁равна полупериметру треугольника ABC.

Доказательство. Пусть Т₂ и Т₃ - точки касания вневписанной окружности с прямыми АВ и ВС соответственно (рис. 1). Тогда СТ₁ = СТ₃, ВТ₂ = ВТ₃ (как отрезки касательных, проведенных из одной точки к окружности) и периметр треугольника ABC равен

2р=АС+ СТ₃ + BT₃ + АВ=АС+СТ₁ + АВ + ВТ₂ = AT₁ + АТ₂.

А так как АТ₁ = АТ₂, то р = AT₁ , что и требовалось доказать.

Свойство 3. Площадь S треугольника ABC равна S = r_а(р – а).

Доказательство. Легко видеть, что

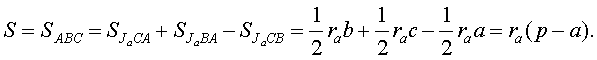
Покажем применение рассмотренных свойств вневписанной окружности к решению задач.

Задача № 1. Докажите формулу Герона для площади треугольника:

Рис. 2

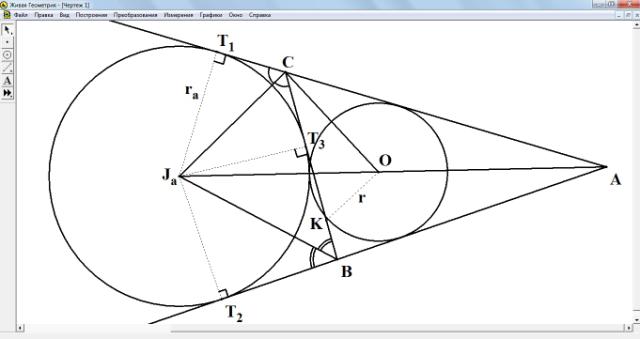
$C:\Users\Артур\Desktop\3.jpg$

Решение. Воспользуемся обозначениями рисунка 2.

Треугольники CJ_aT₁и СОК подобны. Значит,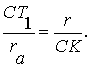

Но СК = р - с, а СТ₁ = р-АС = р - b.

Откуда 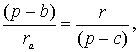или

Но 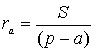(свойство 3), а 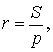значит,

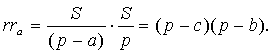
Отсюда и следует формула Герона

Задача № 2. Окружность с центром O касается стороны AB равнобедренного треугольника ABC в точке L, продолжения боковой стороны AC и продолжения основания BC соответственно в K и N . Точка M – середина основания BC.

a) Докажите, что AN = OM

b) Найдите OM, если стороны треугольника ABC равны 13, 13 и 24.

Доказательство:

a) докажем, что AN = OM (рис. 3).

Пусть CBA = β ABN = -β;

Из LBNO: LON = β,KAL =-+ β + β = 2β (по теореме о внешнем угле треугольника) OAL = β

Рис.5

из AOL: AOL = – β, тогда

AON= – β + β = ONMA – прямоугольник AN = OM (диагонали).

Рис. 3

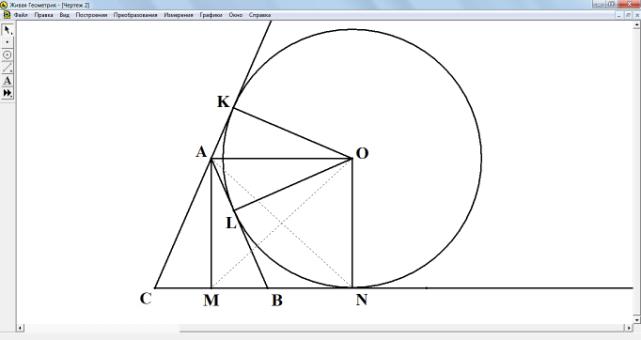
$C:\Users\Артур\Desktop\2.jpg$

b) Найдем OM.

P_ABC= AB + AC + BC = 13 + 13 + 24 = 50;

По свойству касательных имеем: BN = BL, AL = AK; CK = CN = 25 (свойство 2). Из AMB: AM

Т.к. CM = 25, то BN = BL = 1 MN = MB + BN = 13, а т.к. AONM – прямоугольник, то AM + ON = 5;

Из ONM: OM.

Ответ:OM.

Данная задача может быть решена и без использования свойств вневписанной окружности, но при помощи их дальнейшее решение задачи стало очевидно.

Геометрия начинается с треугольника. Две с половиной тысячи лет постоянно открываются его новые свойства. В школьной программе рассматриваются далеко не все свойства вневписанной окружности. В представленной статье рассмотрены некоторые свойства и показано применение вневписанной окружности к решению задач. Данный материал выходит за рамки школьной программы и будет полезен учащимся при подготовке к итоговой аттестации и подготовке к олимпиадам.

Литература:

1. Билецкий, Ю.А. О пользе вневписанной окружности // Квант. - 2001. - №2. – С.28-30.

2. Березин, В.И. Сборник задач для факультативных и внеклассных занятий по математике. – М.: Просвещение, 1985 г.

3. Гнеденко, Б.Г. Энциклопедический словарь юного математика. – М.: Просвещение, 1985 г.

4. Понарин, Я.П. Элементарная геометрия. – М.: МЦНМО, 2004 г.