Магистрант Кабдрахманова
М.Е, к.т.н. Кабылбекова У.М.
Казахский
Агротехнический Университет им.С. Сейфуллина
Применение
преобразования для полосовых фильтров
Свойства Z-преобразования. Важным свойством z-преобразования является
свойство его единственности. Любая последовательность s(k)
однозначно определяется z-изображением в области
его сходимости, и наоборот, однозначно восстанавливается по z-изображению.
Без углубления в теорию, можно констатировать,
что все свойства ДПФ действительны и для z-преобразования.
Отметим некоторые из них.
Линейность: Если s(k)=a*x(k)+b*y(k),
то S=aX(z)+bY(z).
Соответственно z-изображение допустимо
только для анализа линейных систем и сигналов, удовлетворяющих принципу
суперпозиции.
Задержка на n тактов:
y(k)=x(k-n).
Y(z)
= 
k = 
k = z n 
k-n=
=
z n 
m= z n X(z)
Соответственно, умножение z-образа
сигнала на множитель z n
вызывает сдвиг сигнала на n тактов дискретизации.
Рассмотрим на примере эквивалентной схемы
фильтра.
Примеры аппроксимации кривых и разностные
уравнения.
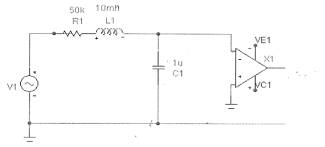
Рис.1 - Электрическая цепь R, L, C,
питаемая синусоидальным напряжением U=UmSin(wt)
Построим
дифференциальное уравнение,
описывающее процессы в приведенной цепи
фильтра.
(1)
или
(2)
Заменив 
на 
и 
на 
, запишем
дифференциальное уравнение
в виде:
(3)
где 
и
- первая
и вторая производные по времени.
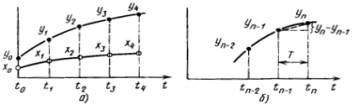
Рис. 2 – Графическое
представление принципа z-преобразования
При интегрировании
такого уравнение с помощью цифровой ЭВМ переменные 
и 
и
производные 
должны представляться
для дискретных моментов времени и в цифровой форме. На рис. 2а показаны дискретные
моменты времени 
и соответствующие этим моментам времени
значения переменных 
и 
, которые с помощью
АЦП могут быть преобразованы в
цифровую форму, производные 
представлены через значения 
для моментов 
(рис. 2б) можно приближенно выразить
производную 
для момента 
(
и через значения 
производную 
:
Аналогично вторую производную можно представить
выражением
После подстановки
выражений 
имеем
Полученные приближенные выражения 
подставим в дифференциальное уравнение (1):
Разрешим полученное выражение относительно 
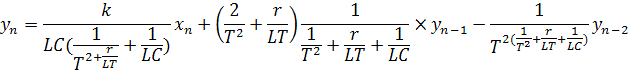
или
(4)
где 
-значения коэффицентов в (3) перед соответствущими переменными.
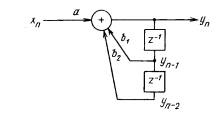
Рис.3 – Схема последовательности вычислений
Последовательность вычислений
для подобных фильтров
удобно представлять в виде схемы, показанной на рис.3.
Здесь над цепями, подходящими к суммирующему элементу, показаны
коэффициенты, с которыми производится суммирование соответствующих переменных; элемент задержки на один тактовый интервал
времени Легко обнаружить соответствие между данной схемой и решением разностного уравнения.