ФИЗИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ И КАЧЕСТВЕННЫЕ ПЕРЕХОДЫ

Перевозников Е.Н. , Скворцов Г.Е.

Перевозников Евгений Николаевич – к.ф-м.н. Санкт-Петербургский торгово-экономический университет.

Скворцов Генрих Евгеньевич – к.ф-м. н. Санкт-Петербургский университет

Дается описание естественной физической неустойчивости. Указывается ее связь с явлениями качественного перехода. Приводятся динамические критерии физической неустойчивости.

Ключевые слова: физическая неустойчивость, критерии, качественные переходы, демонстрационные примеры.

Как правило, в технологиях важно соблюдение режима, отход от него приводит к браку, Поддержание режима обеспечивается контролем устойчивостью по Ляпунову. Однако в физике и других областях важен феномен качественного перехода, или указание острого его варианта- разрушения, взрыва, биологических конфликтов, кризисов, катастроф.

Это явления с положительной обратной связью. Для их обнаружения или инициации необходимо использовать иные, отличные от традиционных , критерии, которые имеют другую теоретическую основу.

Такой основой должна служить теория физической неустойчивости (ФНУ).

Продемонстрируем ее вариант и приведем примеры ее применения.

1.Напомним ряд признаков естественной физической неустойчивости /1/.

1.1 Малые причины - большие следствия (амплитудный признак)

1.2 Большие изменения за малое время (скоростной признак).

1.3 Большие изменения на малых пространственных интервалах (градиентный признак).

1.4 Возникновение нескольких состояний (бифуркация)

1.5 Резонанс.

2.Эти естественные положения составляют основу первого блока признаков ФНУ, назовем его сингулярным.

Если исходить из образа δ- функции и использовать процедуру дифференцирования и интегрирования, то можно конкретизировать сингулярные признаки в виде 5 форм: возьмем за основу скачек ( часто наблюдаемый при различных качественных переходах), для менее интенсивных ФНУ можно поставить в соответствие первый и второй интегралы скачка т.е. уголок и точку перегиба, для интенсивных ФНУ используем производную скачка - δ- функцию, для взрывных ФНУ – производную от δ- функцию.

Все указанные зависимости наблюдаются в физических, химических, биологических, социально-экономических качественных переходах.

3. Второй блок критериев ФНУ образуют указания временных или пространственных интервалов, на которых происходит развитие неустойчивости. В идеале их можно считать нулевыми, однако в реальности они всегда конечны. Их можно назвать интервалами обострения ( временными или пространственными). Для их определения необходимы пространственно- временные модели изменения основных величин, которые, как правило, представляются в виде дифференциальных уравнений.

Далее ограничимся рассмотрением дифференциальных уравнений с временной переменной.

4. Аналитические выражения для сингулярного блока признаков получаются согласно описанию данному в п.2. Они имеют вид:

а) - (скачок)

б) - (бифуркация)

в) при (уголок)

г) при - (δ- образность)

д) - (бесконечнозначность, уплощение)

е) s- нецелое или отрицательное ( степенная сингулярность).

В отличие от теории катастроф, где рассматриваются особенности статических гладких отображений, в теории ФНУ включаются сингулярности любого вида и характера.

Сравнивая ФНУ с ляпуновской неустойчивостью, обнаруживаем связь нейтральности с бифуркационным критерием, Покажем ее на простом примере

(1)

λ> 0 – ляпуновская неустойчивость, λ< 0 – устойчивость, λ=0 нейтральность и одновременно условие бифуркации. Так, что рассматривая критерии нейтральности /1,2,3/ можно одновременно обнаруживать бифуркационную сингулярность Действительно , как показано в /4/, многие качественные переходы описываются N-образной зависимостью. В ней сингулярными точками являются два экстремума (max и min) и точка перегиба. Экстремумы представляют границы качества- изменение структуры, а точка перегиба означает промежуточное состояние при смене структур.

5. Приведем схему выявления ФНУ для дифференциальных моделей:

1) указываются сингулярности правых частей уравнений- действий

( только они могут быть источниками ФНУ);

2) начальные условия соотносятся с сингулярностями (Sing ) для

уточнения условий реализации ФНУ:

3) действия упрощаются в окрестности сингулярности;

4) упрощенные уравнений решаются;

5) из вида решения получаются окончательная форма критериев и время

развития ФНУ.

Продемонстрируем схему на достаточно простых моделях, чтобы был понятен алгоритм.

5.1 Рассмотрим уравнение

,(2)

0 < a < b. На этом примере будет выявлен один из стандартных типов ФНУ.

Согласно схеме указываем sing : х ₁ =а, х ₂ =b, х ₃ → ∞ . Определяем какие из них можно привести к ФНУ с учетом начального условия. Если х ₀ < b,

То из анализа уравнения (2) следует, что x(t) будет стремится к а, достигая этого значения при t→ ∞. Очевидно , sing(а) не реализует ФНУ. Заметим, что если х ₀ < а, то х возрастает, т.е . имеем неустойчивость по Ляпунову. Величина b служит границей качества; при х ₀ > b реализуется sing х ₃. Этот результат получается из качественного анализа.

Уравнение (2) имеет решение

.(3)

Ясно, что х→ ∞ при t→ t _c, поскольку х-а > x-b,

.(4)

Из решения видна граничная роль начального условия.

Укажем, что можно не получать решения (3), а воспользоваться общей формулой

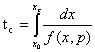.(5)

Здесь f – действие уравнения , х _с - sing, который приводит к ФНУ.

В рассмотренном примере очевидно , х _с =х _с3 = ∞.

Заметим, что выявленная ФНУ, аналогична режиму с обострением , изученному в /5/ для более сложных моделей.

5.2 Второй простой пример, существенно отличающийся от первого, - уравнение с запаздыванием

,(6)

ν – декремент, τ – время запаздывания ( начальное условие в линейной модели - любое). Решаем (6) спектральным методом. Основой его служит спектральное уравнение

,(7)

s- спектральный параметр, он взят с минусом для упрощения выкладок

( при этом правая полуплоскость соответствует затуханию – диссипации, а левая - усилению). Уравнение (7) равносильно двум для вещественной и мнимой частей

.(8)

Из этих уравнений получаем удобную связь

,(9)

с помощью которой два уравнения сводятся к одному для y.

Ясно, что sing в (8) - это нули тригонометрических функций. Дальнейший анализ сводится к определению решений уравнений (8) – траекторий х(с), у(с), и их особенностей.

Очевидно, при с=0, z=1. С ростом с спектральная траектория z(c) вещественна и движется вправо согласно зависимости .

Это означает, что режим чисто диссипативный и декремент возрастает.

Для определения особенностей и сопряженных с ними неустойчивостей и качественных переходов полезно свести (7) к дифференциальному уравнению

.(10)

Сингулярности – нули числителя и знаменателя. В числителе представляют интерес нули вещественной и мнимой частей порознь.

Нуль знаменателя

,(11)

С учетом (8) получаем х _с =е, с₁=1/е. Это вертикальная бифуркация- физическая неустойчивость, она связана с появлением мнимой части. Последнее означает качественный переход: в системе возникла колебательная составляющая, одновременно вследствие движения траекторий влево, рост декремента сменился его убыванием.

Прослеживая путь траектории, отмечаем наличие максимума у при

с₂ ≈0.6, у≈1.6, х≈1.15. Этот max(y) обозначен нулем ; c ним можно связать режим наблюдаемости колебаний, поскольку у/х≈1.13 .

Далее с ростом с траектория достигает мнимой оси при с ₃= 1.57, у=1. Нуль вещественной части y cos(cy) означает физическая неустойчивость – резонанс, если при этом значении запаздывания произвести гармоническое воздействие частотой с₃.Продвижение в левую полуплоскость- переход от затухания к усилению исходно диссипативной системы следует признать качественным переходом (КП).

Основная траектория исчезает при (су) =π ; этому соответствует ФНУ и КП. Последовательность ФНУ возникает при пересечении мнимой оси следующими ветвями при с₄ =3/2 π, с₅ =5/2 π, ... .

По этому анализу сделаем ряд замечаний. Указанные особенности и соответствующие им эффекты симметричны относительно вертикальной оси при изменении знака ν в (6) на плюс. В этом случае имеем переход от изначально активной системы к диссипативной при с₃. Подобные обратные превращения имеют прикладное значение. Указанные эффекты наблюдались в технических системах с запаздыванием. Однако в физике авторы не нашли о них сведений.

6. Приведем примеры моделей с внешним гармоническим воздействием,

. При таком воздействии на гармонический осциллятор с частотой ω и малым затуханием, как хорошо известно, получается резонанс , если . Такой режим следует считать ФНУ.

Еще одним видом ФНУ является хаотический режим /6/. Динамический хаос свидетельствует о том, что даже система с двумя степенями свободы при внешнем гармоническом воздействии становится неработоспособной.

Одним из самых конструктивных критериев ФНУ такого рода служит критерий Мельникова /6/. Для динамической модели

,(12)

согласно /6/, критерий возможного хаоса имеет вид

.(13)

В заключении следует подчеркнуть фундаментальный характер физической неустойчивости. Она, наряду с технологической неустойчивостью , охватывает все поле возможностей нерегулярных, в том или ином смысле, состояний и режимов. Прежде всего ФНУ охватывает все виды качественных переходов ( фазовых, структурных, динамических). Она позволяет их обнаружить и либо устранить, либо использовать с существенным результатом. Большая роль ФНУ заключается в возможном выявлении физических эффектов. Она реализовывалась ранее /8/.

Литература

1. Перевозников Е.Н.,Скворцов Г.Е.,Письма ЖТФ, т.5, вып.22,1979, №5, с.17.

2. Скворцов Г.Е., Перевозников Е.Н., ЖТФ, т.52, вып.12,1982, с.2353.

3. Перевозников Е.Н. Изв.Вузов,Физика, №10, 2006, с.34.

4. Скворцов Г.Е., Письма ЖТФ, т.24,вып.19,1998,с.7.

5. Режимы с обострением, Сб. М., 1998, с…..

6. Кузнецов С.П., Динамический хаос, ФМЛ, М.,2006, с….

7. Ланда П.С., Нелинейные колебания и волны, М. Наука-физматгиз, 1997,с 624.

8. Скворцов Г.Е., Письма ЖТФ,1997,т.23,вып.22; 1999,т25,вып.1; 1999, т.25, вып.7.