Физика/2. Физика твердого тела

Широков А. Е.

Национальный исследовательский университет «МИЭТ»

«Невидимые объекты» в длинноволновом пределе

В последнее время широкое распространение приобретают метаматериалы, обладающие уникальными электрофизическими, оптическими свойствами, наноматериалы с заданными свойствами, позволяющими использовать эти материалы как в прикладных целях, так и в фундаментальных исследованиях. В силу широкой востребованности этих материалов задача моделирования их электрофизических, оптических свойств превратилась в стандартную инженерную задачу. В данной работе исследованы особые объекты типа дефектов в одномерном кристалле, кристаллический потенциал которого моделируется обобщённым потенциалом Кронига-Пенни с удвоенным периодом (см. рис. 1). Оказывается, что эти объекты оказываются невидимыми в длинноволновом приближении (при , ), что выражается в резонансах коэффициента прохождения (коэффициент прохождения тождественно равен 1 в вышеуказанном пределе), при этом эти объекты не могут быть описаны в рамках т.н. безотражательных потенциалов [2].

В статье [1] продемонстрирована возможность существования подобных объектов в одномерном кристалле в модели сильной связи. Эти объекты - т.н. скрытые пары дефектов (СКП) – характеризуются антисимметричными потенциалами, расположенными в неэквивалентных узлах решётки, причём коэффициент прохождения для этой СКП равен тождественно единице без какого-либо фазового множителя, а связанные состояния отсутствуют. Как известно, размер дефекта в длинноволновом приближении (МЭМ) может существенно отличаться от соответствующего микроскопического. Поскольку в длинноволновом приближении одиночному дефекту соответствует дельта-барьер, то аномальной прозрачности СПД в этом приближении соответствует схлопывание дельта-барьеров, соответствующих паре дефектов. В рамках МЭМ заданной СПД может быть сопоставлена некая постоянная «эффективная длина» пары дефектов, в случае же выхода за рамки приближения МЭМ эта длина оказывается зависящей от энергии (волнового вектора).

Рис.1 Атомный потенциал 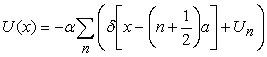в обобщенной модели Кронига-Пенни. В (31) 2a – период решетки, , . 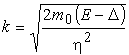в области “ям” и 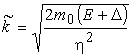в области “барьеров”. Обобщенная модель переходит в стандартную модель Кронига-Пенни в пределе .

На рисунке 2 приведена модель СПД, исследовавшаяся в этой работе. В области I решение уравнения Шредингера имеет вид , в области II между дефектами - , в области III - . Здесь - блоховские волновые функции, соответствующие волнам, бегущим в противоположных направлениях. В данной модели для коэффициента отражения в случае СПД получаем:

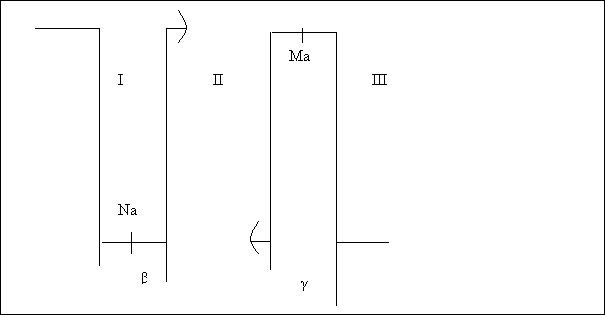
Рисунок 2. Модель двух дефектов, расположенных в неэквивалентных узлах. Дефекты находятся в точках x= (N+1/2)a и x=(M-1/2)a. Потенциалы дефектов и . СПД соответствует условие , , , , - значения блоховских волновых функций в точках, где находятся дефекты.

(1)

Здесь

,(2),

- производная блоховской функции на границах ячеек,

,

,

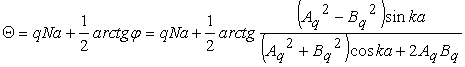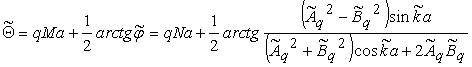, - значения блоховской волновой функции на границе полуячеек (см. рис. 1).

В длинноволновом приближении (что эквивалентно приближению эффективной массы МЭМ) аналогичная пара дефектов с антисимметричными потенциалами (соответствует условию (2)) моделируется двумя дельта-барьерами, отстоящими друг от друга на некотором расстоянии L (длина дефекта в приближении МЭМ), см. рис. 3.

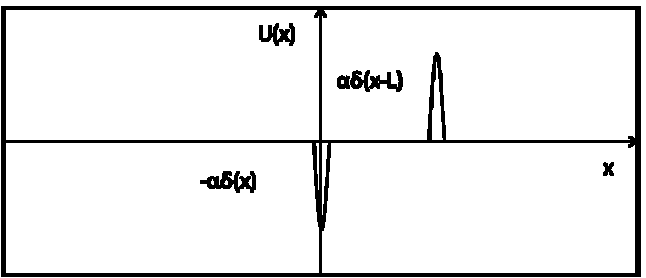
Рис. 3 Два дефекта с антисимметрическими потенциалами в модели непрерывной среды (предел МЭМ).

В этой модели для коэффициента отражения получаем:

(3)

Из формулы (3) видим, что тождественно равен нулю, если L=0. В рассматриваемой нами модели (1) коэффициент отражения при , 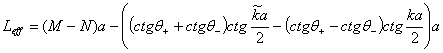также может обращаться в ноль в пределах применимости МЭМ . Это и соответствует СПД, невидимой в длинноволновом приближении.

Литература

1. Горбацевич А. “Тёмная материя” в кристаллах: объекты, невидимые в низкоэнергетическом рассеянии. / А.А. Горбацевич // Письма в ЖЭТФ — 2006. — т. 84. — № 11. — с. 708-713.

2. Лэм Дж., Введение в теорию солитонов, пер. с англ., М.: Мир, 1983.