Физика/7. Оптика

Д. ф.-м. н. Астапенко В.А., д. ф.-м. н. Головинский П.А., Яковец А.В.

Московский физико-технический институт (государственный университет)

Оптический контроль переноса возбуждения между квантовыми точками в двухуровневой модели

Исследуется возможность оптического контроля переноса возбуждения между квантовыми точками с помощью эффекта Штарка для разработки оптической элементной базы в квантовой информатике.

Основные свойства ферстеровского переноса энергии между экситонными состояниями в полупроводниках могут быть проанализированы на основе модели системы с двумя резонирующими уровнями [1]. Особенности переноса энергии зависят от соотношения между величиной энергии диполь-дипольного взаимодействия и шириной уровней. Если доминирует кулоновское взаимодействие, то перенос энергии от донора к акцептору идет когерентно, и образуется новое состояние, являющееся суперпозицией состояний подсистем. Если ширина акцепторного уровня больше ширины донорного уровня и величины взаимодействия, то перенос осуществляется некогерентно, диссипативные процессы в доноре идут медленно, а диссипация происходит быстро в акцепторе. Этот предельный случай соответствует классической модели Ферстера.

При детальном описании подобных процессов используются различные модельные гамильтонианы. Важно, кроме кулоновского взаимодействия между состояниями в соседних квантовых точках, включить в описание сдвиг уровней энергии за счет оптического эффекта Штарка во внешнем нерезонансном поле и спонтанный распад возбужденных уровней за счет излучения фотонов и фононов. Для построения соответствующей квантовой модели рассмотрим схему энергетических уровней, представленную на рис. 1, и запишем соответствующий модельный гамильтониан.

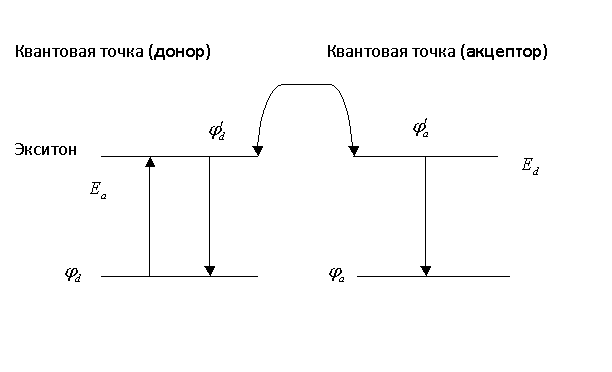
Рис. 1. Схема энергетических уровней, фотовозбуждения, релаксации и переноса энергии в системе двух квантовых точек.

Состояния объединенной системы из двух квантовых точек есть и : – основное состояние донорной квантовой точки, – основное состояние акцептора, – основное состояние экситона донора, – основное состояние экситона акцептора. В этом базисе волновая функция системы:

, (1)

а эффективный гамильтониан двух взаимодействующих квантовых точек можно записать в виде

, (2)

где выделена диагональная часть

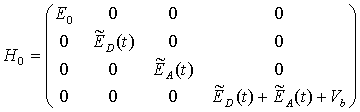, (3)

соответствующая изолированным квантовым точкам с учетом оптического эффекта Штарка, и оператор взаимодействия

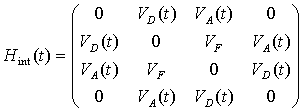, (4)

учитывающий взаимодействие точек между собой и внешним лазерным полем. Здесь – энергия основного состояния системы; , – энергия системы, в которой возбуждено экситонное состояние донора; , – энергия системы, в которой возбуждено экситонное состояние акцептора. Взаимодействие точек с лазерным импульсом описывается оператором , – величина кулоновского взаимодействия, – спонтанная ширина экситонного состояния донора, – спонтанная ширина экситонного состояния акцептора. Штарковский сдвиг энергии экситона донора – , а штарковский сдвиг энергии экситона акцептора – . Оба они медленно меняются со временем. – сдвиг биэкситонного уровня, т.е. двух экситонов в разных квантовых точках за счет кулоновского взаимодействия между ними. Структура гамильтониана учитывает возможность возбуждения (девозбуждения) биэкситона путем поглощения (излучения) двух фотонов разными квантовыми точками.

При учете только фестеровского взаимодействия гамильтониан совпадает с использованным в работе [2], а если учесть кулоновское взаимодействие и ширину уровней, то соответствующий гамильтониан фигурирует в [3]. В последнем случае модель допускает точное аналитическое решение, однако использованный в [3] формализм матрицы плотности для такой формы гамильтониана является избыточным, поскольку в нем присутствует только поперечная релаксация, а более простой и эквивалентный формализм имеет вид уравнения Шредингера с учетом затухания. Аналитическое решение задачи о резонансных переходах между квантовыми точками под действием лазерного излучения без учета затухания приведено в работе [4]. Хотя в ней рассмотрен физически иной механизм передачи возбуждения за счет туннельного перехода электрона, сам формализм пригоден и для описания резонансной передачи энергии от экситона к экситону в соседней квантовой точке. Гамильтониан (2) позволяет описать, в частности, и все исследованные ранее случаи.

Если в исходном состоянии в донорной квантовой точке уже имеется экситон, то перенос возбуждения к акцептору описывается укороченной системой уравнений для состояний и :

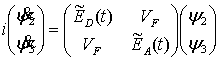. (5)

В случае, когда сдвиг уровней меняется со временем, ,, где – энергия донорного уровня, – энергия акцепторного уровня при расстройке резонанса . Мы учитываем сдвиг уровней в параметрах и .

В этих обозначениях уравнение Шредингера принимает вид:

, (6)

.

Полученная система уравнений описывает прямой и обратный когерентный резонансный перенос возбуждения с учетом отстройки резонанса и затухания состояний, связанного с их релаксацией [5].

Для CdSe зависимость частоты переходов от радиуса нанокристаллов может быть аппроксимирована в первом приближении следующей зависимостью [6]:

При нерезонансном воздействии на систему пикосекундных импульсов и сопоставимо малых временах релаксации экситонов управление медленно меняющимся сдвигом энергии уровней за время развития всего динамического процесса сводится к управлению расстройкой резонанса . Пикосекундные импульсы можно считать квазигармоническими, и они могут быть заданы в виде произведения гармонической несущей волны и медленно меняющейся гауссовой огибающей:

, (7)

. (8)

Для нахождения численного решения уравнения Шредингера для трехуровневой системы использовался пакет Mathcad [7]. Характерные параметры системы составляют эВ, мэВ [8], а амплитуда лазерного возмущения системы эВ при длительности импульса пс, пс.

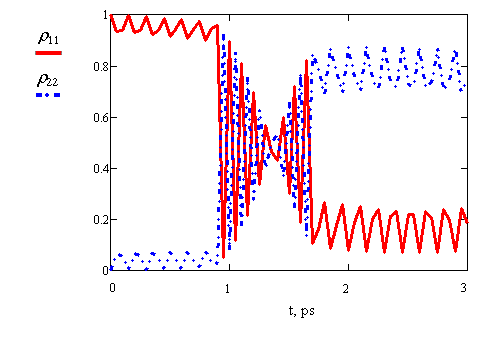
Рис. 2. Изменение заселенности донорного и акцепторного состояний квантовых точек при квазипересечении уровней, управляемом лазерным полем.

На рис. 2 показан результат расчета переноса возбуждения при квазипересечении уровней в управляемом эффекте Штарка. Время изменения лазерного поля составляет 0.8 пс. Мелкие осцилляции показывают многократный частично обратимый перенос энергии между донором и акцептором. Максимальная заселенность акцепторного уровня составляет 0.93 и достигается за 1.7 пс. Соответствующий лазерный импульс, управляющий оптическим Штарковским сдвигом уровней, должен иметь почти прямоугольную «П»-образную форму огибающей, т.е. его включение и выключение должно происходить за фемтосекунды.

Работа выполнена при финансовой поддержке РФФИ (грант 13-07-00270) и Министерства образования и науки Российской Федерации в рамках базовой части Государственного заказа (№ 2014/120-1940).

Литература:

[1] В. М. Агранович, М. Д. Галанин. Перенос энергии электронного возбуждения в конденсированных средах (М., Наука, 1978).

[2] A. Nazir, D. W. Lovett, S. D. Barrett, J. Y. Reina, G. A. D. Briggs. Anticrossing in Forster coupled quantum dots, Phys. Rev. B, 71, 045334 (2005).

[3] C. King, B. Barbiellini, D. Moser, V. Renugopalakrishnan. Exactly soluble model of resonant energy transfer between molecules, Phys. Rev. B, 85, 125106 (2012).

[4] А. В. Цуканов, Л. А. Опенов. Резонансные переходы электрона между полупроводниковыми квантовыми точками под действием лазерного излучения. ФТП, 38, 94 (2004).

[5] S. C. Rand. Nonlinear and quantum optics using the density matrix (Oxford, Oxford University Press, 2010)

[6] В.А. Астапенко. Взаимодействие излучения с атомами и наночастицами, Интеллект, 2010 г.

[7] В. Очков. Mathcad 14 для студентов, инженеров и конструкторов. БХВ-Петербург, 2007 г.

[8] A. Nazir, B. W. Lovett, G. A. D.  Briggs. Controlling excitonic entanglement in quantum dots through the optical Stark effect, Phys. Rev. A, 70, 05231 (2004).