Физика/7. Оптика

Одаренко Е. Н., Сашкова Я. В.

Харьковский национальный университет радиоэлектроники, Украина

МОДЕЛИРОВАНИЕ РАССЕЯНИЯ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ НА ЦИЛИНДРИЧЕСКИХ МНОГОСЛОЙНЫХ СТРУКТУРАХ

Задачи о рассеянии электромагнитных волн занимают значительное место при исследовании физических свойств различных электродинамических структур. В частности, важную роль играют задачи о рассеянии излучения цилиндрическими и сферическими объектами. Их решения нашли свое применение во многих областях науки и техники: в медицине, радиолокации, оптоволоконной технике и др. Кроме того, в последнее время значительное внимание исследователей привлекают такие системы, как цилиндрические omniguide-волноводы [1]. Особенность такой линии передачи состоит в реализации полного внутреннего отражения при произвольных углах падения на многослойную оболочку волновода.

Другая область изучения цилиндрических объектов с диэлектрическим покрытием – это так называемая оптическая маскировка (cloaking) [2]. Здесь используются уникальные физические свойства метаматериалов, которые имеют отрицательный показатель преломления.

При решении отдельных задач по разработке оптических приборов находят широкое применение устройства градиентной оптики, в том числе и цилиндрические линзы. В этом случае показатель преломления среды изменяется в зависимости от координат по определенному закону. Один из методов расчета таких систем основан на стратификации неоднородной среды. В этом случае непрерывное изменение показателя преломления заменяется кусочно-однородным [3].

В данной работе на основе решения задачи дифракции плоской волны на бесконечном многослойном цилиндре создан расчетный проект для визуализации пространственного распределения поля и определения электродинамических характеристик системы. В постановке задачи не накладываются ограничения на количество слоев, их материальные параметры и геометрические размеры. Допускается также наличие слоев с отрицательным показателем преломления, т. е. содержащих метаматериалы. Такого рода структуры могут применяться, в частности, для создания градиентных линз с необычными оптическими свойствами [3, 4].

Рассматривается бесконечный диэлектрический многослойный цилиндр (количество слоев ). Образующая цилиндра параллельна координатной оси Оz (рис. 1). Нумерация показателей преломления слоев начинается с сердцевины цилиндра. Вдоль положительного направления оси Оx на структуру падает плоская монохроматическая волна с параллельной поляризацией (вектор напряженности электрического поля параллелен образующей цилиндра).

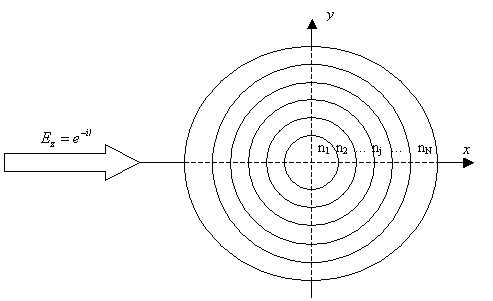
Рисунок 1 – Падение волны на многослойный цилиндр

Для записи полей в различных областях исследуемой системы используется стандартное представление через цилиндрические функции:

· Волна, падающая на цилиндр 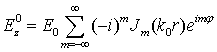(1)

· Рассеянная цилиндром волна 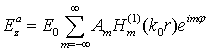(2)

· Поле в сердцевине цилиндра 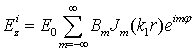(3)

· Поле внутри j-го слоя 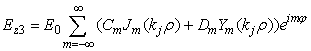(4)

Здесь: – функция Бесселя; – функция Неймана; – функция Ханкеля 1-го рода; , , – волновые числа окружающей среды, сердцевины цилиндра и -го слоя соответственно; , , , – амплитудные коэффициенты.

Для нахождения неизвестных амплитудных коэффициентов используются граничные условия. Однако, даже для небольшого количества слоев аналитические выражения для коэффициентов оказываются весьма сложными. Поэтому для реализации расчетного алгоритма необходимо выбрать методику, которая бы упрощала процесс вычислений. Поскольку расчетная модель создавалась в пакете компьютерной алгебры, то наиболее приемлемым вариантом оказалось использование матричной формы записи системы линейных алгебраических уравнений:

, (5)

где – матрица системы; – вектор-столбец неизвестных коэффициентов; – вектор-столбец правых частей неоднородной системы уравнений. Матрица системы представляется следующим образом:

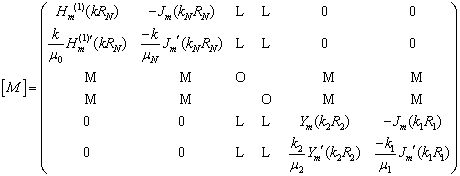. (6)

Тогда решение системы уравнений сводится к простой операции, которая состоит из вычисления обратной матрицы системы и перемножения результата на вектор-столбец правых частей системы:

. (8)

На рис. 2 представлены результаты расчета пространственного распределения интенсивности электрического поля длиной волны λ = 10 мкм, рассеянного многослойным цилиндром. Количество слоев N = 10, диаметр сердцевины D = 2 мкм, толщина слоев 0,1 мкм (рис. 2а) и 0,3 мкм (рис 2б). Показатель преломления изменяется по закону 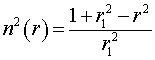, – фокусное расстояние.

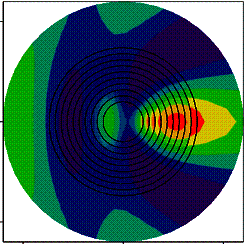
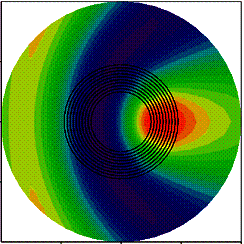
(а) (б)

Рисунок 2 – Результаты расчета

Рассмотренный в работе закон изменения показателя преломления модифицированной линзы Люнеберга соответствует фокусировке света внутри линзы. Предложенная методика позволяет значительно сократить время расчета пространственного распределения рассеянного поля по сравнению со стандартной процедурой решения системы линейных алгебраических уравнений. Видимо, причина этого состоит в эффективности алгоритмов работы с матрицами, заложенных в пакетах компьютерной алгебры.

Полученные результаты позволяют определить закономерности изменения фокусирующих свойств многослойной цилиндрической линзы при изменении ее материальных параметров и геометрических размеров. В частности, изменение параметров системы приводит к уменьшению или увеличению фокусного расстояния цилиндрической линзы.

Список источников

1. Pochi Yeh, Amnon Yariv. Theory of Bragg fiber // Optical Society of America –1978 –Vol. 68, No. 9. – pp. 1196 –1201.

2. Веселаго В.Г. Электродинамика материалов с отрицательным коэффициентом преломления // УФН. – 2003. – №7. – с. 790–794.

3. Gordon J. M. Spherical gradient-index lenses as perfect imaging and maximum power transfer devices // Applied Optics. – 2000. – V.39, Nо. 22. – P. 3825–3832.

4. Котляр В.В., Личманов М.А. Дифракция плоской электромагнитной волны на градиентном диэлектрическом цилиндре // Компьютерная оптика. – 2003. – Вып. 25 – С. 11–15.