Хуанган Н

Хуанган Н., Исабек Т.К., Демин В.Ф.

Қарағанды мемлекеттік техникалық университеті, Қазақстан

Ходжаев Р.Р.

ЖШС «ГеоМарк» ғылыми зерттеу орталығы, Қазақстан

Өзара әсер ететін жарықшақтардың

кернеулік күйі жайлы мәселе

Біз бір жарықшақ – әр түрлі өлшемді кеуектердің айналасындағы кернеуді қарастырып келдік. Әрине егер кеуектер арасындағы қашықтық айтарлықтай үлкен болған жағдайда мұндай тәсіл заңды болып табылады. Қатты денелердегі, әсіресе кен жынысындағы кеуектер көп жағдайда тығыз орналасады да, олардың кернеулік өріс әсерін ескермеуге болмайды. Бұл параграфта біз екі терең айналма саңылауы бар салмақты жарты жазықтықтың кернеулік күйін негізге ала отырып, дискретті шекті шарттар әдісімен өзара әсер ететін саңылаулар мәселесін шешу жолдарының бірін қарастырамыз [1]. Бұл шешімді әр түрлі контурлы кеуектерге қолдануға болатындығы белгілі.

Екі жақты байланыс салалары үшін, осы жұмыста қарастырылып отырған жеке мәселе үшін де, дәлірек айтқанда, екі бірдей терең айналма саңылауы бар салмақты жарты жазықтықтың күйі жайлы мәселені тиімді шешу жолдарын Д. И. Шерман ұсынды [2, 3]. Ондағы ұсынылатын әдіс қарастырылатын мәселені екі жақты байланыс салаларына, ал соңғысын шешкеннен кейін көмекші функция үшін екінші текті Фредгольм теңдігіне келтіруге мүмкіндік береді, көмекші функция тек бір айналма саңылауға қатысты енгізіледі. Фредгольмнің бұл интегралдық теңдігі көмекші функцияның Фурье кешендік қатарына ыдырау коэффициентіне қатысты оны шекміз сызфықтық алгебралық теңдіктер жүйесіне келтіру жолымен шешіледі. Бұл жүйедегі зерттеулер мәселені шешудің маңызды әрі еңбек сыйымды бөлігін құрайды.

Мәселені осыған ұқсас шешу А. С. Космодамианскийде де бар [4], мұнда саңылау контурында анықталатын кешендік ауыспалы функциялар мен [2] Фурье кешендік қатарына ыдырайды да, жоғарыда аталған функцияларды шешу мәселелері Галеркин әдісімен жүргізіледі. Мақалада ұсынылған өзара әсер ететін терең айналма саңылауларды анықтау әдісі жоғарыда аталған екі әдіске қарағанда төмендегі алғышартты басшылыққа алады.

Айтарлықтай ұзын екі бірдей айналма қазбасы бар серпімді изотропты массивті – тегіс деформацияланған күйді қарастырайық. [2]-ден байқағанымыздай, мұндай массивтің кернеулік күйі туралы мәселе екі айналма саңылауы бар шексіз облысқа арналған тегіс серпімділік теориясына келтіріледі, ондағы әрекет ететін сығу күші шексіздікке вертикаль бағыт бойынша қарқындылықпен, ал горизонталь бағыт бойынша қарқындылықпен өтеді, мұнда r - орта тығыздығы; l - бүйірден керу

коэффициенті; Н – айналма саңылау центрінің орталық сызығынан күндізгі бетке дейінгі қашықтық. Саңылаулар радиусын бірге тең деп, ал ал саңылаулар центрі арасындағы қашықтықты 2×а деп аламыз. Декартты координаталар жүйесі 1-суретке сәйкес жасалды.

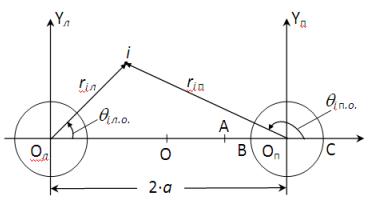
2-сурет

Қарастырылып отырған массивтің кернеулік күйі қазба жүргізгенге дейінгі кернеу өрістері мен қазба жүргізу нәтижесінде пайда болған кернеу өрісінің қосындысынан шығады. Бұл өрістердің алғашқысы мынадай мәндермен сипатталады

. (4.76)

Осы және келесі түсіндірулерде сығушы кернеуді теріс, ал созушы кернеуді оң деп аламыз. Әрі қарай, бірінші кезеңде, екінші саңылаудың әсерін ескерусіз, саңылаулар бірінің (мысалы, сол жақ саңылау) айналасындағы екінші және суммалық өрісті анықтаймыз. Яғни сол жақ саңылаудың кернеу өрісі бір жақты байланыс облысында анықталады. Оның шешімі белгілі [5] және кернеудің бір радиусының шеңбері үшін мынаған тең болады:

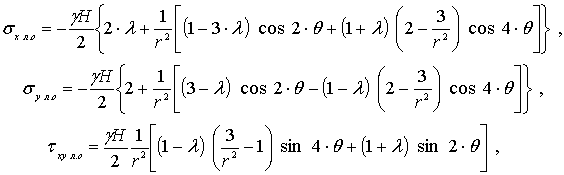(4.77)

мұнда , , - сол жақ (жалғыз) саңылаудың сәйкес келетін қалыпты және тангенциалды кернеуі.

Әрі қарай оң жақ саңылаудың кернеулік өрісін оған әсер ететін сол жақ саңылаудағы кернеулік өрісті ескерумен анықтаймыз, яғни екі жақты байланысқа арналған кернеулік өрісті анықтаймыз.

Бұл кезеңді орындау үшін оң жақ чсаңылаудың бірінші кернеулік өрісінің орнына оған сол жақ саңылаудың әсер етуінен массивте пайда болатын кернеулік өрісті аламыз (4.77). Алайда бұл өрісті жалпы түрде алатын болсақ, онда Колосов – Мусхелишвили әдістері жалпы алғанда қолданыссыз қалады, өйткені бұл жағдай Лаплас операторы (j - Эр кернеулер функциясы) гармониялық функция болып табылмайды. Бұл кемшіліктерге жол бермеу үшін, сол жақ шеңберге арналған кернеулік өрісті жалпы түрде алмай, жазықтықтың әр нүктесі үшін жеке-жеке (дискретті түрде) анықтаймыз. Осылайша, оң жақ саңылаудың i нүктесіне арналған бірінші кернеулік өріс мына формулалар бойынша анықталады:

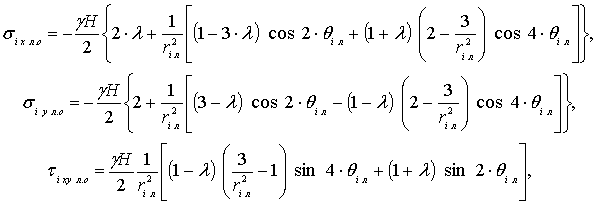(4.78)

, , - сол жақ саңылаудың i нүктесіне арналған қалыпты және тангенциалды кернеу немесе оң жақ саңылаудың дәл осы нүктесіне арналған бірінші кернеулік өріс; , - сол жақ саңылаудың i нүктесінің полярлық координаталары (радиус және бұрыш).

Бұдан оң жақ саңылау болмаған жағдайда, сол жақ саңылаудың i нүктесінің бірінші кернеулік өрісіне жүктелетін аналитикалық потенциалдарды [5]-ге сәйкес анықтаймыз. Оң жақ шеңбердің АВ доғасы (А – саңылау контурының абциссалар осімен белгіленген қиялысу нүктесі, В – контурдың жылжымалы нүктесі) арқылы берілетін күш мынаған тең:

. (4.79)

s-ны В-мен теңдестіре отырып, (4.79) формуласын былайша өзгертуге болады

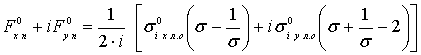. (4.80)

Аналитикалық потенциалдар эллипс контурынан бұл күшті жою мүмкіндігін береді. Басқаша айтқанда, функциясына жауап беру керек, ол мына формула арқала анықталады

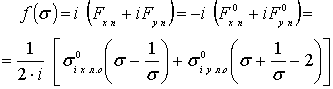. (4.81)

Оны мына теңдік құрамына ендіру

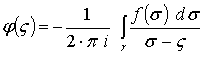(4.82)

үш интегралдың пайда болуына әкеледі:

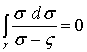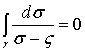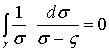; ; . (4.83)

Алғашқы екі нәтиже Кошаның бір шеңберге арналған интегралды теоремасынан шығады, мұнда V оның сыртындағы нүктені белгілейді. Үшінші интеграл арналған формуланы сыртқы облысқа арналған Коша теоремасынан немесе ішкі облысқа арналған есептеулер теоремасынан аламыз.

Бұдан

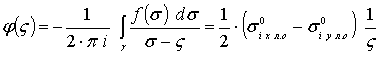. (4.84)

мәнін анықтау үшін мына формуланы қолданамыз:

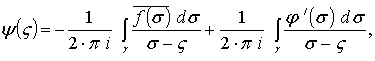(4.85)

мұнда .

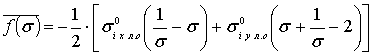Компоненты напряжений в системе координатОң жақ саңылауға арналған x, y координаталар жүйесінлегі кернеу компоненттерін енді мен -дан z-ға дейінгі туындылардан табуға болады,

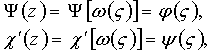(4.86)

болатындығын ескере отырып, алатынымыз

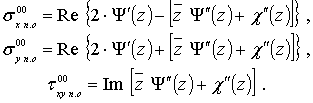(4.87)

Суммарные напряженияОң жақ саңылаудың i нүктесіндегі суммалық кернеуді сол жақ саңылаудың дәл осы нүктесінде оған әсер ететін өрісті (екі жақты байланыс облысының кернеулік өрісі) ескерумен, мына формулалардан анықталады

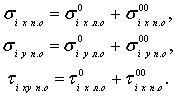(4.88)

Бұдан, (4.78-4.88)-ді ескерумен алатынымыз

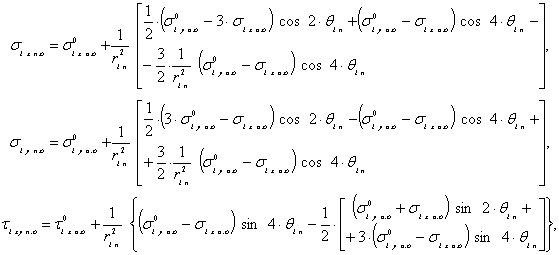(4.89)

мұнда , - оң жақ саңылаудағы i нүктенің полярлық координаталары (радиусы мен бұрышы).

4.1 және 4.2-кестеде бүйірден керу мәні болғанда, саңылаулар () арасындағы О, А, В,С нүктелеріне арналған (4.3-сурет) және кернеу шамалары берілген. [2] пен [4]-те Д. И. Шерман мен А. С. Космодамианский бойынша дәл сол нүктелердегі кернеу шамаларымен салыстырғанда, 1/2×а = 1/4 болғанда, саңылаулар арасындағы қашытық бір саңылау диаметріне, 1/2×а = 1/3 болғанда, диаметр жартысына, 1/2×а = 0,4 болғанда, диаметр ширегіне тең болады.

1-кесте

Нүктелер

[133]сәйкес

мәндері

[135] сәйкес

мәндері

Ұсынылып отырған әдіске сәйкес

мәндері

1/2×а

1/4

1/3

0,4

1/4

1/3

0,4

1/4

1/3

0,4

0,48

0,46

0,00

0,53

0,44

0,00

0,41

0,32

-0,00

0,00

0,49

0,48

0,02

0,01

0,57

0,49

0,04

0,01

0,40

0,32

0,00

0,01

0,40

0,32

0,00

0,63

0,46

0,00

0,67

0,40

0,00

0,55

0,49

0,00

0,50

0,41

0,00

0,39

0,31

0,00

0,49

0,48

0,02

0,01

0,49

0,41

0,00

0,30

0,22

-0,05

0,02

0,59

0,52

0,00

0,63

0,47

0,00

0,62

0,38

0,00

0,62

0,52

0,00

0,46

0,38

0,00

0,36

0,29

0,00

0,61

0,52

-0,01

0,42

0,33

-0,04

-0,02

0,2

0,13

-0,11

-0,06

0,70

0,47

0,00

0,64

0,47

0,00

0,57

0,36

0,00

2-кесте

Нүктелер

[133]сәйкес

мәндері

[135] сәйкес

мәндері

Ұсынылып отырған әдіске сәйкес

мәндері

1/2×а

1/4

1/3

0,4

1/4

1/3

0,4

1/4

1/3

0,4

1,50

1,67

3,02

3,07

2,25

2,37

3,26

3,15

3,26

3,43

4,03

3,26

1,47

1,67

3,07

3,09

2,15

2,38

3,35

3,18

3,24

3,40

3,97

3,38

1,50

1,68

3,07

3,01

2,28

2,46

3,38

3,02

3,64

3,72

4,18

3,04

1,50

1,66

2,72

2,61

2,21

2,29

3,08

2,70

3,11

3,27

3,84

2,21

1,50

1,66

2,72

2,61

2,11

2,29

3,07

2,69

3,06

3,20

3,67

2,88

1,52

1,69

2,76

2,58

2,19

2,42

3,19

2,64

3,35

3,52

3,98

2,68

1,53

1,65

2,41

2,16

2,21

2,89

2,26

2,96

3,11

3,66

2,36

1,53

1,65

2,37

2,14

2,06

2,20

2,76

2,20

2,88

2,99

3,37

2,37

1,55

1,70

2,44

2,16

2,15

2,37

3,00

2,25

3,07

3,31

3,78

2,33

Бұл әдіс сонымен қатар x, y осьтерін бойлай, 2×а_x және 2×а_y қашықтықта орналасқан, әр түрлі конфигурациялы бірнеше саңылауларының контуры жанындағы кернеулік өрісті анықтау мүмкіндігін береді. Бұл ретте шекті жағдайды бірінші саңылаудан екіншіге, т.с.с. () саңылауға дейін кезекпен ауыстыруды ескерумен дискретті шекті жағдайда анықтаудың бастапқы кезеңіндегідей пікірлерді еркін i нүктесі үшін де орындаймыз.

Сонымен қатар оны көлемді мәселелердәі шешуде де, кеуек пен жарықшақтың өзара әсерін есептеуде де қолдануға болады.

Әдебиеттер тізімі:

1. Стрелков С.П. Механика. – М.: Наука, 1957. – 560 с.

2. Абрамович Г.Н. Прикладная газовая динамика. – М.: Наука, 1969. – 824 с.

3. Справочник. Рудничная вентиляция / под ред. К. Э. Ушакова. – М.: Наука, 1988. – 440 с.

4. Абрамов Ф.А. Рудничная аэрогазодинамика. – М.: Наука, 1972. – 272 с.

5. Петросян А.Э. Выделение метана в угольных шахтах. – М.: Наука, 1975.