Колесник М. В., Ладієва Л. Р.

Національний технічний університет України «Київський політехнічний інститут», Україна

Оптимальне керування процесом гранулювання у псевдозрідженому шарі

Математичне моделювання об’єкта керування

При складанні формального опису об’єкта моделювання в основу математичної моделі процесу висушування було покладено основи законів збереження маси і теплової енергії матеріальних потоків. Для отримання моделі застосовуються формули, які характеризують тепло- і масопередачу.

Рівняння матеріального балансу, що складається з входів і виходів матеріальних потоків, які протікають в апараті, зображується наступним чином:

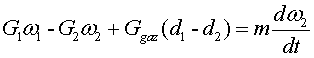, (1)

де m – маса матеріалу, яка знаходиться в барабанному грануляторі-сушарці в даний момент, кг/с; w₁– вологість матеріалу на вході в апарат, кг/кг; w₂– вологість матеріалу на виході з апарату, кг/кг; G₁ – кількість початкового вологого матеріалу, кг/с; G₂ – кількість кінцевого висушеного матеріалу, кг/с; G_gaz – витрата сушильного агенту, кг/с; d₁ – вологовміст сушильного агенту на вході в апарат, кг/кг; d₂– вологовміст сушильного агенту на виході з апарату, кг/кг;

Рівняння теплового балансу, що складається з входів і виходів теплових потоків, які протікають в апараті, зображується наступним чином:

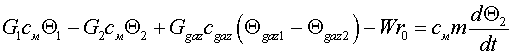, (2)

де с_м – теплоємність матеріалу, кДж/(кг*К); Θ₁ – температура матеріалу на вході в апарат, К; Θ₂ – температура матеріалу на виході з апарату, К; c_gaz – теплоємність сушильного агенту, кДж/(кг*К); Θ_gaz1 – температура сушильного агенту на вході в апарат, К; Θ_gaz2 – температура сушильного агенту на виході з апарату, К; – кількість вологи, яка видаляється при сушці, кг/с; r₀ – питома теплота пароутворення води при 0ºС, кДж/кг;

Кількість вологи, що видаляється при сушці дорівнює різниці вагів вологого і сухого матеріалу:

₀ (3)

З рівняння (3) виразимо G₂ і підставимо в рівняння (1) та (2), відповідно спростивши їх, отримаємо рівняння (4) та (5):

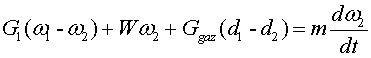(4)

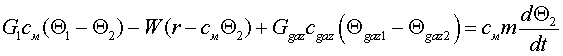(5)

Кількість вологи, що видаляється при сушці можна розписати як різницю парціальних тисків перегрітої рідини і пари, одразу лінеаризуємо це рівняння:

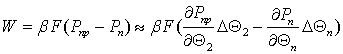(6)

Згрупуємо ці рівняння і отримаємо:

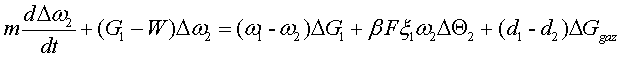(7)

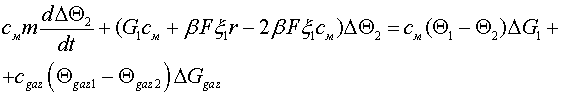, (8)

де .

Вибір критерію і знаходження необхідних умов оптимальності

Для розрахунку застосовуємо принцип максимуму [1]. Він використовується, коли керуючі впливи не належать до класу неперервних функції чи коли на змінні задачі накладаються обмеження типу нерівність. Для лінійних систем принцип максимуму є достатньою умовою оптимальності. Обираємо квадратичний інтегральний критерій оптимальності.

Критерій оптимальності для даного процесу представляється наступним чином:

.

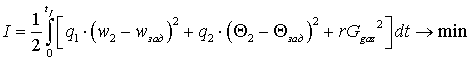Запишемо Гамільтоніан наступним чином:

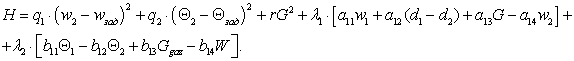
Отримали спряжені рівняння і умови трансверсальності, оптимальне керування:

;

.

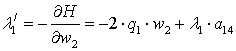
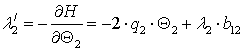
Розрахунок оптимального програмного керування

_{Алгоритм розрахунку оптимального програмного керування:}

_{1. За постійного керування, розрахувати в прямому часі математичну модель процесу;}

_{2. В зворотному часі розв’язати спряжену систему;}

_{3. Знаходимо оптимальне керування;}

_{4. Повертаємось до пункту 1 з оптимальним керування і розраховуємо траєкторію переходу.}

Розрахунок оптимального керування зі зворотнім зв’язком

Використовуємо лінійний регулятор стану з інтегральною складовою, який має вигляд:

₀

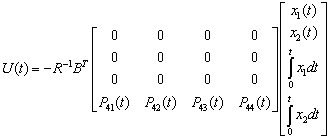251652608

Складемо матрицю стану А та керування В

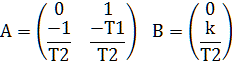
Отримавши А та В, запишемо рівняння Ріккаті у матричній формі:

Отримаємо систему нелінійних диференційних рівнянь:

На основі математичної моделі процесу гранулювання у псевдозрідженому шарі, з використанням принципу максимуму, знайдено оптимальне керування за методами зворотного зв’язку та програмного керування для підтримання заданої температури висушеного матеріалу на виході апарату та мінімізації керуючого впливу. В результаті порівняння оптимального керування за методом зворотного зв’язку та методом програмного керування, можна зробити висновок, що кращий результат оптимальної траєкторії досягнуто за допомогою метода зворотного зв’язку з інтегральною складовою.

Література

1. Ладієва Л. Р. Оптимальне керування системами [Текст] : навч. посіб. – К.: НМЦ ВО. –2000. – 187 с.: іл. – Бібліогр.: с. 185-186. – 200 пр. – ISBN 966-622-026-1.