Амирбеков Р.К.
Карагандинский
экономический университет Казпотребсоюза, Казахстан
Использование алгоритма
Дейкстры при создании информационной системы управления процессами прохождения
нарядов в телекоммуникационной компании
Одним из основополагающих требований, предъявляемых к эффективно
функционирующим социо-техническим системам, к которым относятся
телекоммуникационные компании, является рациональное управление, которого, в
свою очередь, невозможно достичь без проведения качественного планирования. В рамках
планирования деятельности системы чаще всего решается задача рационального
использования ресурсов. Задача же управления потоком поступающих заявок
зачастую остается без должного
внимания. Имея большую численность клиентов, телекоммуникационная компания, при
предоставлении по договору сервисных работ в глобальных сетях, обеспечивают
необходимый минимум условий техподдержки. Для конкуренции на рынке
телекоммуникационных услуг решающее значение имеет качество предоставляемого
сервиса, которое зависит как от работы установленного оборудования, так и от
качества работы системы технической поддержки.
С момента обращения
пользователя в службу поддержки за помощью, клиент снимает с себя
ответственность и может абсолютно ничего не делать, поскольку при разборе
ситуации виноватой все равно окажется компания, предоставляющая набор сервисов.
Таким образом, уже сама служба поддержки становится заинтересованной в
качественной и быстрой обработке заявки, разграничении полномочий и
упорядочении деятельности сотрудников при оказании помощи пользователям.
Последовательность обработки обращений пользователей должна помочь
сосредоточить силы сотрудников компании на наиболее важных и критичных, но
вместе с тем не оставить без должного внимания и все остальные обращения пользователей.
Поэтому все обращения должны быть оценены и приоритезированы специалистами
службы поддержки (диспетчерами). Это связано с тем, что невозможно одинаково
быстро отработать все заявки, тем более что часть из них и не требует быстрого
решения. Поэтому ранжирование заявок способствует более гибкому управлению
ресурсами и позволяет устранять критичные проблемы. Происходит своеобразное
разделение труда. Пользователи тоже участвуют в такого рода разделении труда,
поскольку обращаются за помощью только к операторам и не отвлекают своими
вопросами остальных сотрудников компании, давая им возможность работать более
продуктивно.
Таким образом, если абонент обратился в службу поддержки за
помощью, его выслушают и на своем
уровне оператор попробует решить проблему. Оператор (1-я линия поддержки) -
регистрирует обращение, при возможности помогает пользователю самостоятельно,
либо эскалирует (передаёт и контролирует выполнение) заявку на вторую линию
поддержки. Вторая линия поддержки — получает заявки от первой линии, работает
по ним, при необходимости привлекая к решению проблемы специалистов из смежных
отделов (тестировщики или системные администраторы).
Специалисты третьей линии проверяют все аппаратные подключения на
стороне телекоммуникационной компании и, при необходимости, выезжают к абоненту
с соответствующим аппаратным обеспечением. Заявка от абонента будет закрыта
оператором первой линии по отчету, поступившему от инженера третьей линии.
Скорость устранения неисправностей связи у клиентов зависит от квалификации
операторов первой и второй линии. Количество специалистов третьей линии
ограничено и соответственно увеличивается время реакции на заявку и
восстановление соединения. Основной работой исполняемого процесса является
обработка заявки. Обработка заявки включает этапы формирования наряда на
устранение неисправности и передачи описания ошибки и всей истории работы с
клиентом на предыдущих линиях. После устранения неисправности заявку необходимо
закрыть. Между тем, проведение анализа, прогнозирования и планирования потока
заявок позволит повысить общую эффективность функционирования системы
обслуживания.
Алгоритм голландского ученого Эдсгера Дейкстры находит все
кратчайшие пути из одной изначально заданной вершины графа до всех
остальных. С его помощью, при наличии всей необходимой информации, можно,
например, узнать какую последовательность дорог лучше использовать, чтобы
добраться из одного адреса до каждого из многих других, или из одного города до
каждого из многих других, или в какие страны выгодней экспортировать нефть и т.
п. Минусом данного метода является невозможность обработки графов, в которых
имеются ребра с отрицательным весом, т. е. если, например, некоторая система
предусматривает убыточные для Вашей фирмы маршруты, то для работы с ней следует
воспользоваться отличным от алгоритма Дейкстры методом.
Для реализации алгоритма понадобиться два массива:
логический visited для хранения информации о посещенных вершинах и
численный distance, в который будут заноситься найденные кратчайшие пути.
Итак, имеется граф G=(V, E). Каждая из вершин входящих во
множество V, изначально отмечена как не посещенная, т. е. элементам
массива visited присвоено значение false. Поскольку самые
выгодные пути только предстоит найти, в каждый элемент вектора distance
записывается такое число, которое заведомо больше любого потенциального пути
(обычно это число называют бесконечностью, но в программе используют, например
максимальное значение конкретного типа данных). В качестве исходного пункта
выбирается вершина s и ей приписывается нулевой путь: distance[s]←0,
т. к. нет ребра из s в s (метод не предусматривает петель).
Далее, находятся все соседние вершины (в которые есть ребро из s) [пусть
таковыми будут t и u] и поочередно исследуются, а именно
вычисляется стоимость маршрута из s поочередно в каждую из них:
·
distance[t]=distance[s]+вес инцидентного s и t ребра;
·
distance[u]=distance[s]+вес инцидентного s и u ребра.
Но вполне вероятно, что в ту или иную вершину
из s существует
несколько путей, поэтому цену пути в такую вершину в массиве distance придется
пересматривать, тогда наибольшее (неоптимальное) значение игнорируется, а
наименьшее ставиться в соответствие вершине.
После обработки смежных с s вершин она помечается как посещенная:visited[s]←true,
и активной становится та вершина, путь из s в которую минимален. Допустим, путь из s в u короче, чем
из s в t, следовательно, вершина uстановиться активной и выше описанным образом
исследуются ее соседи, за исключением вершины s. Далее u помечается
как пройденная: visited[u]←true,
активной становится вершина t и вся процедура повторяется для нее. Алгоритм
Дейкстры продолжается до тех пор, пока все доступные из s вершины не будут исследованы.
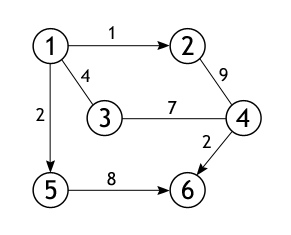
Теперь на конкретном графе проследим работу алгоритма, найдем все
кратчайшие пути между и стоковой и всеми остальными вершинами. Размер
(количество ребер) изображенного ниже графа равен 7 (|E|=7), а порядок
(количество вершин) – 6 (|V|=6). Это взвешенный граф, каждому из его ребер
поставлено в соответствие некоторое числовое значение, поэтому ценность
маршрута необязательно определяется числом ребер, лежащих между парой вершин.
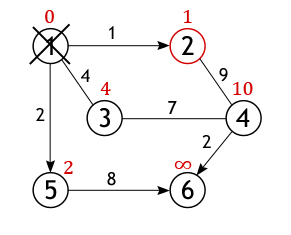
Из всех вершин входящих во множество V выберем одну, ту,
от которой необходимо найти кратчайшие пути до остальных доступных вершин.
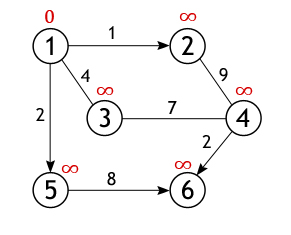
Пусть таковой будет вершина 1. Длина пути до всех вершин, кроме первой,
изначально равна бесконечности, а до нее – 0, т. к. граф не имеет петель.
У вершины 1 ровно 3 соседа (вершины 2, 3, 5),
и чтобы вычислить длину пути до них нужно сложить вес дуг, лежащих между
вершинами: 1 и 2, 1 и 3, 1 и 5 со
значением первой вершины (с нулем):
·
2←1+0
·
3←4+0
·
5←2+0
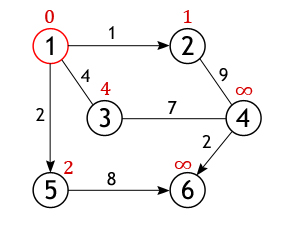
Как уже отмечалось, получившиеся значения присваиваются вершинам,
лишь в том случае если они «лучше» (меньше) тех которые значатся на настоящий
момент. А так как каждое из трех чисел меньше бесконечности, они становятся
новыми величинами, определяющими длину пути из вершины 1 до
вершин 2, 3 и 5.
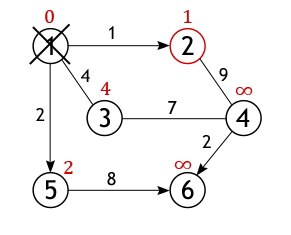
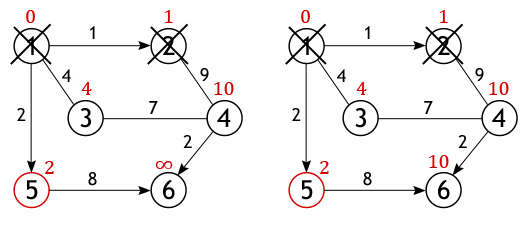
Далее, активная вершина помечается как посещенная, статус
«активной» (красный круг) переходит к одной из ее соседок, а именно к
вершине 2, поскольку она ближайшая к ранее активной вершине.
У вершины 2 всего
один не рассмотренный сосед (вершина 1 помечена как посещенная), расстояние до
которого из нее равно 9, но нам необходимо вычислить длину пути из истоковой
вершины, для чего нужно сложить величину приписанную вершине 2 с весом дуги из
нее в вершину 4:
·
4←1+9
Условие «краткости» (10<∞)
выполняется, следовательно, вершина 4 получает новое значение длины
пути.
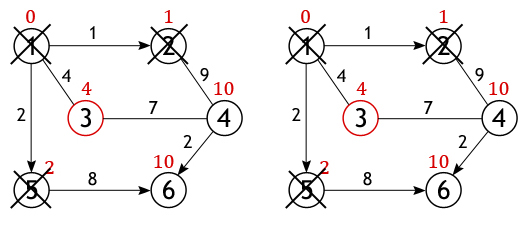
Вершина 2 перестает быть активной,
также как и вершина 1 удаляется из списка не посещённых. Теперь тем
же способом исследуются соседи вершины 5, и вычисляется расстояние до них.
Когда дело доходит до осмотра соседей вершины 3, то тут важно не ошибиться, т. к. вершина 4 уже была
исследована и расстояние одного из возможных путей из истока до нее вычислено.
Если двигаться в нее через вершину 3, то путь составит 4+7=11, а
11>10, поэтому новое значение игнорируется, старое остается.
Та же ситуация выходит и с вершиной 6. Значение самого близкого пути до нее из вершины 1 равно 10, а оно
получается только в том случае если идти через вершину 5.
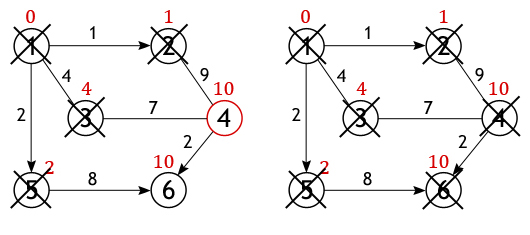
Когда все вершины графа, либо все те, что
доступны из истока будут помечены как посещенные, тогда работа алгоритма
Дейкстры завершится и все найденные пути будут кратчайшими. Так, например,
будет выглядеть список самых оптимальных расстояний лежащих между вершиной 1 и
всеми остальными вершинами, рассматриваемого графа:
1→1=0
1→2=1
1→3=4
1→4=10
1→5=2
1→6=10
В программе, находящий ближайшие пути между
вершинами посредством метода Дейкстры, граф будет представлен в виде не
бинарной матрицы смежности. Вместо единиц в ней будут выставлены веса ребер,
функция нулей останется прежней: показывать, между какими вершинами нет ребер
или же они есть, но отрицательно направленны.
По результатам решения задачи прогнозирования, учитывая колебания
входных потоков заявок на обслуживание, а также различный состав проходимых
заявками элементов системы, возникает задача оптимального распределения
планируемых потоков по временным интервалам обслуживания. Поэтому, разработка
соответствующего оптимизационного алгоритма позволит улучшить эффективность
функционирования системы центра обслуживания, оптимизируя работу по приему
заявок и распределению нарядов по исполнителям, следовательно, является
актуальной задачей.
Литература
1. "Алгоритмы построение и анализ", Кормен Т., Лейзерсон Ч.,
Ривест Р., Штайн К., – Москва, Санкт-Петербург, Киев, 2005 – 1292 с.
2. Зябиров Э.В., Токарев С.П., Федосеева Л.И. МЕТОДЫ ОПРЕДЕЛЕНИЯ КРАТЧАЙШЕГО
ПУТИ МЕЖДУ ВЕРШИНАМИ ГРАФА // Успехи современного естествознания. – 2011. – № 7
– стр. 113-114
3.
Эдриан Пейн, переводчик С. Кривошеин,
Руководство по СRM. Путь к совершенствованию менеджмента клиентов.(Handbook
of CRM: Achieving Excellence in Customer Management)
4. Автоматизированная система. Обзоры, методики,
внедрение. Другие связанные с CRM вопросы.[on-line]: http://www.marketing.spb.ru/soft/crm/index.htm