Технические науки/1. Металлургия
Д. т. н. Кабаков
З.К., Мазина И.Ю.
Череповецкий государственный университет, Россия
Тесты для
численных решений задачи затвердевания металла
При решении
задач, связанных с изучением затвердевания и охлаждения слитков, отливаемых в
изложницы, и заготовок, отливаемых на МНЛЗ, используют численные методы, в
частности, метод конечных разностей. При этом возникает погрешность, зависящая
от параметров численных алгоритмов. Как показывает анализ публикаций, при
моделировании процесса затвердевания и охлаждения слитков и заготовок недостаточно
внимания уделяется вопросу выбора параметров численных методов, при которых
погрешность не превышает допустимой. Возможно, этот пробел возникает в связи с
отсутствием тестов – точных решений задачи затвердевания (задачи Стефана).
В данной
работе представлены тесты и методика тестирования численных методов решения
задачи затвердевания с использованием тестов, выбираемых для конкретных условий
использования результатов решения задачи затвердевания. При разработке тестов
использовали математическую формулировку одномерной задачи о затвердевании
полуограниченного массива расплава (задачи Стефана) с гладкой границей раздела
фаз при граничных условиях I рода, которая
выглядит следующим образом:
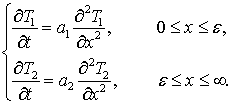
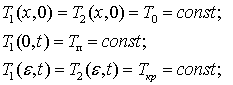
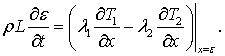
Здесь индекс 1 относит переменные к твердой корке,
индекс 2 – к расплаву.
Данная задача
имеет точное решение [1]:
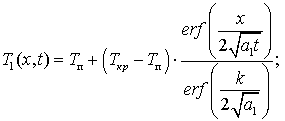
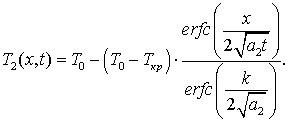(1)
, (2)
где 
– корень уравнения
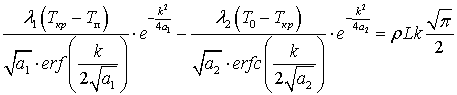. (3)
В формулах
(1)-(3) использованы следующие обозначения:
и 
– теплопроводность
твердой и жидкой фазы, 
и 
– теплоемкость
твердой и жидкой фазы, 
– плотность,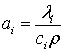 
–
температуропроводность (
– твердая фаза, 
– жидкая фаза), L – удельная
теплота кристаллизации, 
– температура
поверхности, Tкр – температура кристаллизации, T0 – начальная температура расплава,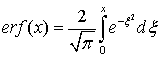 
; 
.
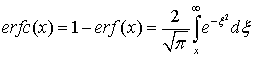Учитывая, что
главным результатом практической задачи затвердевания является толщина корки,
которая в точном решении определяется величиной коэффициента затвердевания, в
данной работе было решено составить таблицу коэффициентов затвердевания для
различных исходных данных (температурных характеристик и теплофизических
свойств металлов).
При
разработке теста выполнили переход к безразмерным величинам:
, 
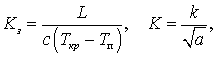
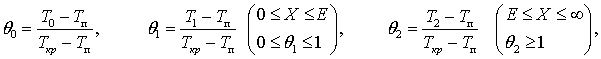
где 
– безразмерный
критерий времени Фурье, Х –
безразмерная координата, Е –
безразмерная толщина корки, S – характерный размер, Kз – критерий затвердевания, 
– безразмерная
начальная температура, 
– безразмерная
температура для твердой корки, 
– безразмерная
температура для расплава. Решение задачи Стефана в безразмерных величинах имеет
вид:
,
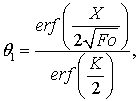
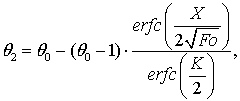
где K – корень уравнения
.
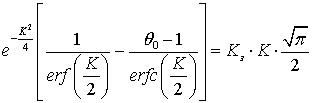Пределы
изменения величины Kз определили с помощью расчета критерия затвердевания
для стали и алюминия. Эти значения составили 0,66 и 6,47 соответственно. Поэтому
для разработки теста в качестве значений критерия затвердевания использовали
числовую последовательность от 0,5 до 6,5 с шагом 0,5.
Для оценки величины 
рассчитали значения
безразмерной начальной температуры для расплава алюминия с величинами перегрева
(
) 10 ºС и 50 ºС при температуре поверхности 600
ºС (
= 1,18 и 1,83 соответственно) и при температуре поверхности
60 ºС (
= 1,02 и 1,08 соответственно). Затем приняли максимальное
значение безразмерной начальной температуры равным 2, минимальное – 1. В
расчетах варьировали 
с шагом 0,05.
Значения коэффициента K для различных значений 
и Kз
рассчитывались с помощью математического пакета MathCAD. Результаты расчета сведены в таблицу.
Таблица
1.
Значения коэффициента K для
различных 
и Kз.
|
Kз q0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
6,5 |
||||
|
1 |
1,6012 |
1,2401 |
1,0513 |
0,9296 |
0,8425 |
0,7761 |
0,7234 |
0,6802 |
0,6439 |
0,6128 |
0,5859 |
0,5623 |
0,5413 |
||||
|
1,05 |
1,5266 |
1,2016 |
1,0257 |
0,9106 |
0,8274 |
0,7637 |
0,7129 |
0,6710 |
0,6358 |
0,6056 |
0,5794 |
0,5563 |
0,5358 |
||||
|
1,1 |
1,4596 |
1,1655 |
1,0015 |
0,8922 |
0,8128 |
0,7516 |
0,7026 |
0,6621 |
0,6279 |
0,5986 |
0,5730 |
0,5505 |
0,5305 |
||||
|
1,15 |
1,3990 |
1,1315 |
0,9780 |
0,8746 |
0,7987 |
0,7399 |
0,6925 |
0,6533 |
0,6202 |
0,5916 |
0,5668 |
0,5448 |
0,5252 |
||||
|
1,2 |
1,3437 |
1,0994 |
0,9556 |
0,8576 |
0,7850 |
0,7284 |
0,6827 |
0,6448 |
0,6126 |
0,5848 |
0,5606 |
0,5391 |
0,5200 |
||||
|
1,25 |
1,2931 |
1,0692 |
0,9343 |
0,8411 |
0,7717 |
0,7173 |
0,6732 |
0,6364 |
0,6052 |
0,5782 |
0,5545 |
0,5336 |
0,5149 |
||||
|
1,3 |
1,2465 |
1,0405 |
0,9138 |
0,8252 |
0,7588 |
0,7064 |
0,6638 |
0,6282 |
0,5979 |
0,5716 |
0,5485 |
0,5281 |
0,5099 |
||||
|
1,35 |
1,2034 |
1,0134 |
0,8941 |
0,8099 |
0,7462 |
0,6959 |
0,6547 |
0,6202 |
0,5907 |
0,5651 |
0,5427 |
0,5228 |
0,5049 |
||||
|
1,4 |
1,1634 |
0,9876 |
0,8752 |
0,7951 |
0,7341 |
0,6856 |
0,6458 |
0,6123 |
0,5837 |
0,5588 |
0,5369 |
0,5175 |
0,5000 |
||||
|
1,45 |
1,1261 |
0,9631 |
0,8570 |
0,7807 |
0,7222 |
0,6755 |
0,6370 |
0,6046 |
0,5768 |
0,5526 |
0,5312 |
0,5123 |
0,4952 |
||||
|
1,5 |
1,0913 |
0,9397 |
0,8396 |
0,7668 |
0,7107 |
0,6657 |
0,6285 |
0,5971 |
0,5701 |
0,5465 |
0,5257 |
0,5071 |
0,4905 |
||||
|
1,55 |
1,0586 |
0,9174 |
0,8228 |
0,7534 |
0,6995 |
0,6561 |
0,6202 |
0,5897 |
0,5634 |
0,5405 |
0,5202 |
0,5021 |
0,4858 |
||||
|
1,6 |
1,0280 |
0,8962 |
0,8066 |
0,7403 |
0,6887 |
0,6468 |
0,6120 |
0,5825 |
0,5569 |
0,5346 |
0,5148 |
0,4971 |
0,4812 |
||||
|
1,65 |
0,9990 |
0,8759 |
0,7910 |
0,7277 |
0,6781 |
0,6377 |
0,6040 |
0,5754 |
0,5506 |
0,5288 |
0,5095 |
0,4922 |
0,4766 |
||||
|
1,7 |
0,9719 |
0,8565 |
0,7760 |
0,7155 |
0,6678 |
0,6288 |
0,5962 |
0,5684 |
0,5443 |
0,5231 |
0,5043 |
0,4874 |
0,4722 |
||||
|
1,75 |
0,9461 |
0,8379 |
0,7615 |
0,7036 |
0,6577 |
0,6202 |
0,5886 |
0,5616 |
0,5381 |
0,5175 |
0,4991 |
0,4827 |
0,4678 |
||||
|
1,8 |
0,9218 |
0,8200 |
0,7474 |
0,6921 |
0,6480 |
0,6117 |
0,5812 |
0,5549 |
0,5321 |
0,5120 |
0,4941 |
0,4780 |
0,4634 |
||||
|
1,85 |
0,8986 |
0,8029 |
0,7339 |
0,6809 |
0,6385 |
0,6034 |
0,5738 |
0,5484 |
0,5262 |
0,5066 |
0,4891 |
0,4734 |
0,4591 |
||||
|
1,9 |
0,8767 |
0,7865 |
0,7208 |
0,6700 |
0,6292 |
0,5954 |
0,5667 |
0,5420 |
0,5204 |
0,5013 |
0,4842 |
0,4689 |
0,4549 |
||||
|
1,95 |
0,8558 |
0,7707 |
0,7082 |
0,6595 |
0,6202 |
0,5875 |
0,5597 |
0,5357 |
0,5147 |
0,4961 |
0,4794 |
0,4644 |
0,4508 |
||||
|
2 |
0,8359 |
0,7555 |
0,6959 |
0,6492 |
0,6114 |
0,5798 |
0,5528 |
0,5295 |
0,5091 |
0,4909 |
0,4747 |
0,4600 |
0,4467 |
Порядок тестирования с использованием точных решений (таблицы
1) следующий:
1). Выбор исходных данных для тестирования конкретной
одномерной задачи затвердевания.
2). Расчет
значений 
, Kз и выбор в таблице 
и 
близких к 
и Kз, из
условия 
и 
.
3).
Определение значения K по таблице и вычисление коэффициента затвердевания 
.
4). Расчет
точного значения толщины корки 
.
5).
Численное решение задачи Стефана для исходных данных, для которых 
и 
.
6).
Сравнение численного решения с точным e*, исследование
величины среднеквадратичной ошибки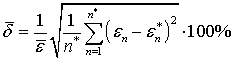 
, где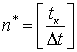 
, 
– результат
моделирования роста корки в момент времени n, 
– точное решение в момент времени n, n – номер текущего момента времени, 
– шаг дискретизации
времени в численном методе решения, 
– продолжительность
роста корки.
Таким
образом, разработаны тесты и методика тестирования численных решений задачи
затвердевания. Тесты применимы для значений безразмерной начальной температуры 
и критерия
затвердевания 
Список литературы
1. Любов Б.Я. Теория кристаллизации в больших объемах.
– М.: Наука, 1975.- С. 256.