Технические науки/2. Механика
К.т.н.
Гладський М.М., к.т.н. Фролов В.К., Сабибіна О.О.
Національний
технічний університет України «КПІ»
Про
визначення параметрів непропорційності циклу деформування
Відомо,
що для створення моделі пластичності при циклічному навантажуванні потрібна
кількісна оцінка ступеню непропорційності навантажування. Для цього
використовували різні величини, такі, як напруження, повну деформацію та
пластичну деформацію. Оскільки повна деформація складається з пружної та
пластичної компонент, а пружна деформація лінійно пов’язана з напруженням, то,
тільки напруження та пластична деформація є незалежними величинами.
В
роботі [1] було детально проаналізовані підходи до побудови параметру
непропорційності через напруження та пластичну деформацію. В роботі зроблено
висновок про те, що і мікроскопічні, і макроскопічні спостереження
підтверджують доцільність використання пластичної деформації при визначенні
параметру непропорційності. Тому саме такі підходи наведено в цій роботі.
Розвиток
досліджень в цьому напрямку пов’язаний з роботами Макдауела, який ввів поняття
ефекту непропорційності циклу та запропонував неперервну міру непропорційності ![]() , що застосовувалася до тензору швидкостей деформацій [2], а
пізніше до тензору пластичних деформацій [3]:
, що застосовувалася до тензору швидкостей деформацій [2], а
пізніше до тензору пластичних деформацій [3]:
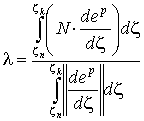
де ![]() - одиничний вектор в
напрямку максимального розмаху пластичної деформації;
- одиничний вектор в
напрямку максимального розмаху пластичної деформації; ![]() - накопичена
пластична деформація на початку та в кінці блоку навантажування. Згідно [3]
коефіцієнт непропорційності визначається виразом:
- накопичена
пластична деформація на початку та в кінці блоку навантажування. Згідно [3]
коефіцієнт непропорційності визначається виразом:
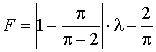 (1)
(1)
Не
дивлячись на те, що коефіцієнт непропорційності у вигляді (1) успішно
використовувався в роботах [4, 5], відзначались і деякі негативні сторони цього
параметру.
На
основі робіт Макдауела, Дунгом та Сосі був розроблений більш складний вираз для
визначення коефіцієнту непропорційності:
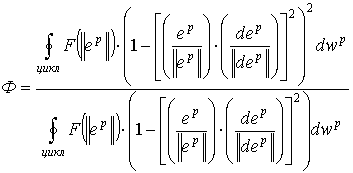
де ![]() - вагова функція,
- вагова функція, ![]() .
.
За
допомогою даного параметру були отримані задовільні результати щодо
прогнозування максимального зміцнення для більш широкого класу непропорційних
траєкторій, однак даний підхід досить складний в застосуванні, до того ж він
потребує знання компонентів вектору напружень ![]() при обчисленні
диференціалу роботи на пластичних деформаціях
при обчисленні
диференціалу роботи на пластичних деформаціях ![]() .
.
Після
робіт Макдауелла ідея про визначення міри, яка б відображала вплив
непропорційності навантажування на процеси деформаційного зміцнення матеріалів,
захопила багатьох дослідників. У результаті чого були запропоновані інші
підходи до побудови параметру непропорційності.
Так, параметри непропорційності, а саме параметр
непропорційності М.В. Бородія та параметр, запропонований в роботі [1] мають багато спільного.
По-перше, так само, як і в роботі Макдауела ці параметри непропорційності
дорівнюють одиниці при навантажуванні по колу і нулю при пропорційному
навантажуванні, для всіх інших траєкторій їх значення лежать між цими
величинами. По-друге, ці параметри непропорційності не містять напружень.
По-третє, через те, що ефекти зміцнення, які спостерігаються в дослідах, як при
деформуванні за траєкторіями повних деформацій, так і при деформуванні за
траєкторіями пластичних деформацій, якісно практично не відрізняються, то
параметри непропорційності не пов'язуються з типом деформацій, а залежать
тільки від геометрії циклу.
Автори роботи [1] запропонували параметр
непропорційності розраховувати за наступною формулою
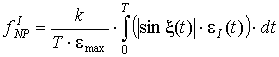 ,
,
де
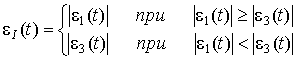 ,
,
![]() ,
,
e1(t), e3(t) – значення максимальної і мінімальної головних
деформацій у момент часу t; Т – тривалість циклу; x(t) – кут між напрямками eІmax та eІ(t). ![]() – константа, яка
необхідна для того, щоб привести значення
– константа, яка
необхідна для того, щоб привести значення ![]() до одиниці при
деформуванні по колу.
до одиниці при
деформуванні по колу.
Для плоских циклічних траєкторій у девіаторному
просторі пластичних деформацій (двовісне навантажування) при фіксованій
максимальній амплітуді циклу параметр непропорційності, запропонований в роботі
[6], записується таким чином:
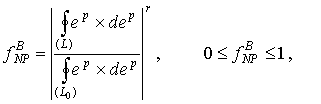 (2)
(2)
де еР, deP
– вектори пластичної деформації та її приросту; L – контур траєкторії деформування в циклі або еквівалентна їй
траєкторія; L0 – контур
траєкторії деформування у вигляді кола, яку можна записати так:
![]() ;
; ![]() .
.
Інтеграли по замкнутому контуру в рівнянні (2)
уявляють собою подвоєні площі в середині даних траєкторій. Тоді для траєкторії
деформування у вигляді кола
![]() ,
,
де ![]() – максимальна
амплітуда циклу.
– максимальна
амплітуда циклу.
Показник степені r для гладких випуклих траєкторій
(наприклад, еліпсів) дорівнює одиниці. В усіх інших випадках його визначають із
виразу
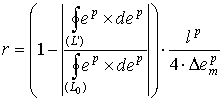 ,
,
де ![]() – максимальний розмах
пластичної деформації;
– максимальний розмах
пластичної деформації; ![]() – довжина траєкторії
пластичної деформації циклу.
– довжина траєкторії
пластичної деформації циклу.
Наведені підходи до визначення параметра
непропорційності дозволяють з достатньою точністю описати процес додаткового
зміцнення нержавіючих сталей 08Х18Н10Т і 316 при циклічному непропорційному
навантажуванні [7]. Не дивлячись на те, що в багатьох випадках результати
розрахунків були близькі між собою і добре співпадали з дослідом, все ж таки
підхід, який запропоновано в роботі [1] має суттєву перевагу. Він дозволяє при
однаковій геометрії траєкторій деформування врахувати вплив домінуючого виду
напруженого стану на додаткове зміцнення матеріалу, яке спостерігається у
досліді. У випадку коли величина деформації зсуву переважає величину осьової
деформації відбувається зниження еквівалентного напруження. Цей
експериментальний факт якісно описується при застосуванні параметра
непропорційності з роботи [1].
Література:
1. Itoh T., Sakane M., Ohnami M., Kida S., Sosie D. F. Dislocation
Structure and Non-Proportional Hardening of Type 304 Stainless Steel. // In:
Proceeding of the 5th International Conference Biaxial-Multiaxial Fatigue and
Fracture, Cracow. - 117. - vol. 1. - pp. 189 – 206.
2. McDowell D. L. A two surface model for transient nonproportional
cyclic plasticity. Pt. 1. Development of appropriate equations. // J. Appl.
Mech. - 1985. - 52. - pp. 298 – 302.
3. McDowell D. L. Simple experimentally motivated cyclic plasticity model
// J. Eng. Mech. – 1987. – 113, № 3. – p. 378-397.
4. Беналлал, Марки. Определяющие уравнения упруго–вязкопластичности для
непропорционального циклического нагружения. // Теоретические основы инженерных
расчетов. - 1988. - №3. - с. 68 – 84.
5. Кучер Н.К. Бородий М.В. Анализ непропорционального циклического
деформирования материалов в рамках эндохронной теории пластичности // Проблемы
прочности – 1993. № 1. – с.24-34.
6. Бородий М. В. К вопросу об определении коэффициента
напропорциональности цикла // Проблемы прочности. - 1995.- № 5-6. -с. 29-38.
7. Shukaev, S., Gladskii, M., Zakhovaiko, A., Panasovskii, K. A method
for low-cycle fatigue life assessment of metallic materials under multiaxial
loading (2008) Strength of Materials
40 (1) PP. 48 – 51 doi: 10.1007/s11223-008-0013-0