УДК 622

В работе представлено регулирование и управление режимов при совместной работе солнечных фотоэлектрических станций (СФЭС) и сети трехфазного переменного тока (СТПТ) (рис.1) [3,5,7]. Применяется преобразователь постоянного тока (ППТ) (рис. 1,г), который состоит из: транзисторов VT1,2; диодов VD1,2,3; конденсаторов С1,2,3 и L1 дросселя. Трехфазный инвертор (ТИ) (рис.1,д) представляет собой мостовое соединение транзисторов VT3¸VT8, на выходе которого с сети переменного тока (СПТ) получены электромагнитно совместимые фазные напряжения U_A, U_B, U_C и токов i_A, i_B, i_C. На рис. 1,е показаны условные направления фазных токов и напряжения с учетом индуктивностей сети LA, LB, LC и э.д.с. е_А, е_В, е_С. ППТ представляет собой недиссипативную буферную цепь [5]. Частота переключения f₀ транзисторов в ППТ в n₀ раз больше частоты СТПТ f₀=n₀f_c. Частота переключения транзисторов VT3¸VT8 в ТИ равна f_c. Транзисторы VT1,2 ППТ (рис.2) закрыты от t=t₀=0 до t=t₁ и от t=t₂ до t=t₃; открыты от t=t₁ до t=t₂ и от t=t₃ до t=t₄. При этом в СПТ от t=t₀ до t=t₂ ток проходит в А, В фазах, а от t=t₂ до t=t₄ - в А, С фазах (рис. 2,з).

На транзисторах VT1,2 импульсы управления U_YVT_1,2 подаются согласно чередованию, показанному на рис. 2,б. С такой же частотой происходит процесс заряда и разряда конденсатора С2. Соответствующая коммутационная функция r_C₂(t) токов заряда и разряда конденсатора С2 показана на рис. 2,в.

Ó Кохреидзе Г.К., Лаошвили Д.П., Пхакадзе Ш.А., 2011

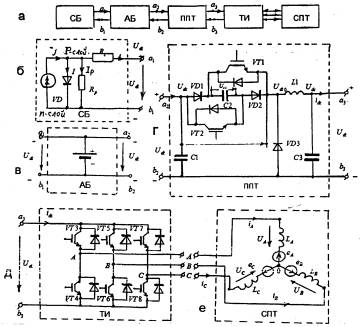
Рис. 1. Структурная и принципиальная электрические схемы элементов единой преобразовательной системы (ЕПС)

Верхние положительные прямоугольные импульсы соответствуют существованию зарядного тока конденсатора С2, а отрицательные прямоугольные импульсы - существованию разрядного тока.

При U_YVT_1,2 =0 имеем r_C₂(t)=1, а при U_YVT_1,2=1имеем r_C₂(t)=-1. Таким образом, r_C₂(t)=

= 1-2 U_YVT_1,2 и U_x=U_dc×r_C₂(t) [3].

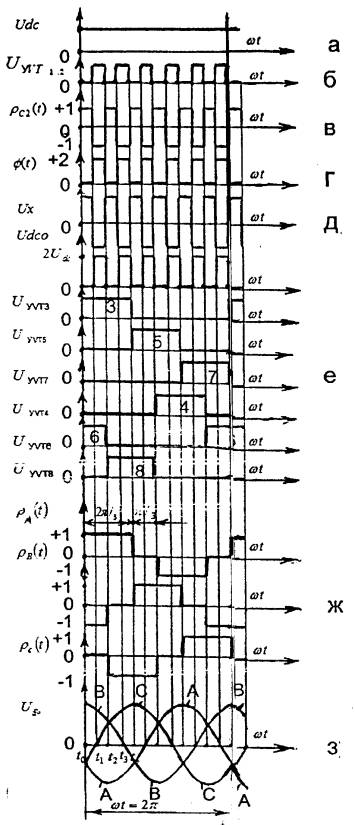
Рис. 2. Волновые диаграммы и коммутационные функции электрических величин ЕПС

Формула напряжения U_dc₀ согласуется с формой коммутационной функции Ф(t), а его мгновенные значения вычисляются так:

U_dc₀ = U_dc× Ф(t) = 2U_dc× U_YVT_1,2 .

Во-вторых, имеем выражение:

U_dc₀ = U_dc+r_C₂(t) × U_C₂(t) = U_dc×Ф(t).

В трехфазном инверторе для обеспечения закона переключения транзисторов VT3¸VT8 принимаем соответствующие расположения импульсов управления (рис. 2,е). Закон изменения коммутационных функций r_A(t), r_B(t), r_C(t) фазных токов ТИ показан на рис. 2,ж. Эти коммутационные функции принимают значения единицы в течение 2p/3w времени, а нулевое - в течение p/3w времени.

Как видно из рис. 1 и 2, в течение одного периода изменения фазных величин СПТ число режимов определяется как: m₀=2n₀, где n₀ - число переключения транзисторов VT1,2 в течение полупериода изменения фазных величин СПТ. В нашем случае получается n₀=6; m₀=12 и f₀=300 Гц.

Топология расчетных схем для всех нечетных режимов структурно одинакова, фиксируются последовательные соединения VD1,2 диодов и конденсатора С2 (рис. 3,а). Аналогично для всех четных режимов расчетные схемы одинаковы, фиксируются последовательные соединения VT1,2 транзисторов и конденсатора С2 (рис. 3,б). Во всех режимах работы происходит переключение силовых VT3¸VT8 транзисторов СИ и фаз СПТ по законам коммутационных функций r_A(t), r_B(t), r_C(t) (рис. 2,ж).

В результате исследования влияния различных условий на выходные характеристики солнечного элемента в уравнение солнечного элемента были включены три дополнительных параметра [4,6]: A, R_S и R_p (рис.1,б)

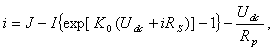(1)

где А - диодный коэффициент, принимающий значения от 1 до 5; R_S - последовательное сопротивление солнечного элемента; R_p - шунтовое сопротивление солнечного элемента; i- выходной ток солнечного элемента; J - фототок, протекающий через p-n переход; I - обратный ток насыщения; U_dc - выходное напряжение солнечного элемента; К - коэффициент Больцмана; Т - абсолютная температура; е - заряд электрона; K₀=e/AKT [1,2] .

Сумма U_dc+iR_S в уравнении (1) представляет собой диодное напряжение U_Д, подающееся на самый солнечный элемент. Если направление тока в модели солнечного элемента принять таким, как показано на рис. 1,б, тогда U_Д=U_dc+iR_S. Если же направление тока обратное, то знак в выражении изменится, т.е. U_Д=U_dc - iR_S. Все параметры солнечного элемента изменяются с изменением температуры, интенсивности освещения и степени радиационного повреждения, и очень трудно измерить параметры I,A,R_S,R_p во всех диапазонах.

Из (1) определим U_dc:

(2)

Подставляя в уравнение (1) отдельно i=0, U_dc=_Udc_×_xx и U_dc=0, i=i_K_.3, получаем уравнения холостого хода и короткого замыкания, решение которых относительно I,J дает:

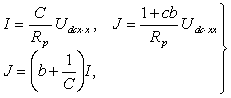(3)

где b= -1+exp(K₀U_{dc. xx});

C=[1-R_pi_K3/U_dc.xx]/[exp(K₀i_K.3R_S)-exp(K₀U_dc.xx)]

. (4)

Подставляя (3) в (2), после преобразования получаем уравнение вольтамперной характеристики солнечного элемента в относительных единицах [4]:

(5)

где

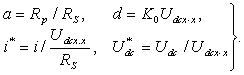(6)

При разложении в ряд Тейлора второго члена правой стороны уравнения (5) и учитывая только первый трехчлен разложения, получим [3]:

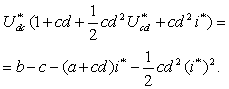(7)

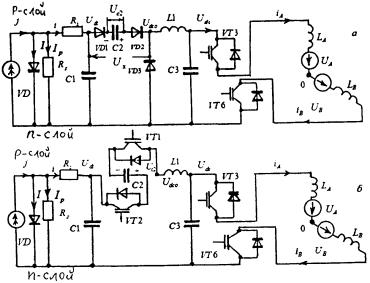
Рис. 3. Топология расчетных схем для нечетных (а) и четных (б) режимов работы единой преобразовательной системы

Из (7) при холостом ходе имеем:

i* =0, (8)

при коротком замыкании имеем:

(9)

Решая уравнение (7) относительно , для интервала 0<i*<i_K_.3, получаем:

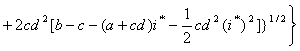. (10)

Для мощности солнечного элемента имеем:

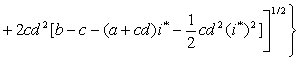. (11)

Для упрощения анализа допускаем, что R_p=R_S. Это даст a=1.

Из (11) при условии dP*/di*=0 получаем уравнение относительно оптимального значения тока нагрузки солнечного элемента :

(12)

где

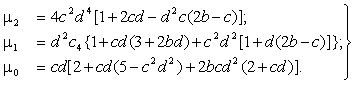(13)

Решая (12) относительно , получаем оптимальное значение тока нагрузки солнечного элемента,при котором мощность достигнет максимального значения

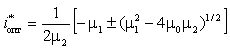. (14)

Учитывая (14) в (10) для оптимального значения напряжения получаем:

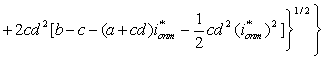. (15)

На основании экспериментальных данных в предлагаемом солнечном элементе заданными являются напряжение холостого хода _Udc_._xx и ток короткого замыкания i_K₃. С учетом этих данных из (4), (6) определим эквивалентные коэффициенты a,b,c,d,m₀,m₁,m₂, оптимального тока и напряжения .

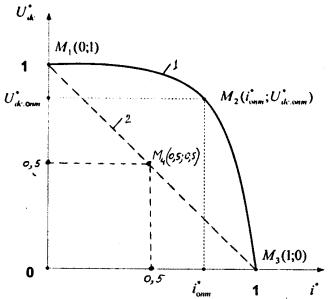
Рис. 4. Вольтамперная характеристика солнечного элемента:

1 - квадратная; 2 - линейная

Таким образом, имеем координаты трех характерных точек M₁(0;1), M₂(;), M₃(1;0) (рис.4) вольтамперной характеристики. На основе координат трех характерных точек М₁,М₂,М₃ и формулы Лагранжа интерполяция вольтамперной характеристики функции дает аналитическое выражение:

, (16)

где

. (17)

Если при разложении в ряд Тейлора второго члена правой стороны уравнения (5) учесть только первый двучлен и произвести аналогичным путем анализ, соответственно получим:

(18)

Уравнение (18) дает возможность построить линейную вольтамперную характеристику солнечного элемента (рис. 4, кривая 2).

Таким образом, в результате проведенной работы предложена полная структурная схема единой преобразовательной системы солнечного элемента - сети трехфазного переменного тока; установлены алгоритмы регулирования и управления процессов; получены квадратное и линейное уравнения вольтамперной характеристики солнечного элемента и определены оптимальные значения напряжений и тока нагрузки.

Список использованной литературы

1. Андреев В.М. Фотоэлектрическое преобразование концентрированного солнечного излучения/В.М.Андреев,В.А.Грилехес,В.Д.Румянцев. Л.:Наука, 1989. - 308 с.

2. Андреев В.М. Фотоэлектрическое преобразование солнечной энергии/В.М.Андреев. - Соросовский образовательный журнал, №7, 1996. Санкт-Петербург, 1996. -93-98 с.

3. Кохреидзе Г.К. Совместная работа солнечной фотоэлектрической станции и сети трехфазоного переменного тока/Г.К.Кохреидзе, Н.Г.Гогинашвили, Ш.А.Пхакадзе. - "Энергия" №3(59), Тбилиси, 2011. - 18-26 с.

4. Раушенбах Г. Справочник по проектированию солнечных батарей/Г.Раушенбах. М.:Энергоатом-издат. 1983. - 358 с.

5. Преобразовательная установка, работающая на сеть переменного тока. В.И.Сенько, У.В.Сенько, Л.И.Сенько, М.Хамрит. - Техническая электродинамика. Ч.1. Киев, 2002. - с. 62-65.

6. Фаренбрух А. Солнечные элементы. Теория и эксперимент/А.Фаренбрух, Р.Бьюб. - М.:Энергоатом-издат, 1987. - 279 с.

7. Якименко Ю.И. Фотоэнергетические системы/Ю.И.Якименко, А.Н.Шмырева, А.В.Богдан. - Техническая электродинамика. Ч.1. Киев, 2000. - 85-92 с.

Получено

Кохреидзе Гиви

Климентьевич

Доктор.техн.наук,

. профессор,

ГТУ,

0102,Цинамдгвришвили 68,

Тбилиси, Грузия,

(+99599) 170014;

(+995 77)102742

E-mail: gmgmgkf @mail.ru

Лаошвили Деми Павлович,

Доктор техн.наук,

профессор

ГТУ,

0102, Цинамдгвришвили 68,

Тбилиси, Грузия,

(+99599) 333399

Пхакадзе Шорена

Автандиловна,

Академический доктор энергетики и электроинженерии

ГТУ,

0102,Цинамдгвришвили 68,

Тбилиси, Грузия,

(+99593) 718388