Химия/8. Кинетика и катализ

A.S. Savenkov, N.Yu. Masalitina, V.V. Rossikhin

National Technical University "Kharkiv Polytechnic Institute"

OXIDATION OF AMMONIA:

EXPERIMENTAL STUDIES AND MATHEMATICAL MODELLING

Currently, the only industrial process for producing nitric acid is the catalytic oxidation of ammonia with oxygen from the air, followed by absorption of nitrogen oxides produced by water. The stage of NH₃ change ratio largely determines the performance of all nitric acid production. The conditions and the quality of its implementation determine the consumption indices of NH₃, input and losses of platinum group metals (PGM) and energetic capabilities of process conditions.

The studies conducted [1–4] justify the assumption about the mechanism of the ammonia catalytic oxidation on platinoid gauzes, give a kinetic model of the reaction, and allow us to determine the conditions of maximum NO output. As the analysis of the bibliography and our experimental research has shown, to ensure the maximum NO selectivity and high intensity of the process it is necessary to maintain external diffusion conditions. At low NH₃ concentrations of the catalyst surface, which is typical for external diffusion conditions, the rates of its oxidation to N₂O and N₂ decrease dramatically and NH₃ selective oxidation to NO takes place [1–4].

One of the shortcomings of previous studies and previously-developed models is the lack of data on the nitrogen oxide formation developed as a byproduct by NH₃ catalytic oxidation in the HNO₃ manufacture process [5–7]. Nitrogen oxide passes through the remaining stages of the HNO₃ production technology unchanged and then is released into the atmosphere. The facilities for the nitric acid manufacture in the CIS countries currently emit about 6.0–7.5 kg of N₂O per year per ton of HNO₃. According to the latest research N₂O is a strong greenhouse gas, whose global warming potential is 310 times greater than the one of CO₂ [8].

Results and discussion. To create a mathematical model of the ammonia oxidation to NO with due consideration of N₂- and N₂O-synthesis, a complex of physicochemical, kinetic and technological research has been carried out.

The essential results of the studies which where carried out at the flow-type facility, and which determined the degree of ammonia oxidation into nitrogen (II) oxide NO and nitrogen (I) oxide N₂O, where the catalyst PGM-gauzes composition – Pt – 90 %, Rh – 10%; wire diameter of catalyst gauzes is d_g = 0.072×10^–3 m. The analysis of the results of the studies shows that along with a high NO output, a simultaneous oxidation of ammonia to N₂O and N₂ is observed, though the rates of these processes are low. At the same time the conversion of NO into N₂ was revealed.

Taking to account the formation of nitrogen (I) oxide for a PGM-catalyst, the stoichiometric basis of ammonia oxidation reaction routes, has the following form:

4NH₃ + 5O₂ 4NO + 6H₂O (1)

4NH₃ + 4O₂ 2N₂O + 6H₂O (2)

4NH₃ + 3O₂ 2N₂ + 6H₂O (3)

2NO N₂ + O₂ (4)

Modelling of the process is reduced to a mathematical description of the process in the catalyst bed considering the assumed reaction mechanism. At a high temperature oxygen on the platinum surface is mainly in the dissociated state. The ammonia adsorption, as well as its dissociation and formation of intermediates interacting with each other, leads to the formation of NO, N₂O, N₂, Н₂О and desorption from the free catalyst surface at 973–1193 K.

In the process of catalysis the ammonia acts as an electron-donor, and oxygen – as an electron-acceptor. Adsorbed О₂ molecules attach electrons from the catalyst surface and turn into oxygen surface atoms (step 1). On step 2 NH₃ molecule donates electrons from the catalyst surface which is not covered with oxygen, N-H bonds are thus weakening and the imido-particles are being formed. On the catalyst surface coated with oxygen, the ammonia forms particles of the imide-type (step 3), which are then recombining and form the nitrogen (step 7). Further addition of oxygen to the imide (steps 4, 5) leads to the formation of NO. Steps 6, 8, and 9 are connected with N₂O, N₂ and Н₂О formation.

The proposed detailed mechanism of the process has been used for deriving kinetic equations, which describe the reactions on the catalyst surface and relate to the formation of O, N₂O, N₂.

The kinetic model of the process of ammonia oxidation for routes I–IV can be written as:

, , , (5)

where r₁, r₂, r₃, r₄ – rates of the routes I–IV; k₁, k₂, k₃, k₄ – kinetic rate constants of the routes I–IV.

The kinetic equations of the ammonia consumption and NO formation reactions have the following form:

(6)

The equations (5–6) were used for description of the ammonia oxidation process on the catalyst PGM-gauzes.

The process in the catalyst bed for external diffusion condition is characterized by a large temperature gradient. At a small distance - a few centimeters in front of the catalyst – the gas is heated by the amount of the adiabatic heating of the reaction mixture from 473 to 1173 K. This can lead to significant longitudinal heat and mass transfer. However, the effective coefficients of longitudinal diffusion and thermal conductivity of the gas phase are small and longitudinal heat transfer is carried out mainly along the solid skeleton of the catalyst bed. When describing the process the influence of the flows arising in non-isothermal boundary layer of multi-component mixture - Stefan flow, thermal diffusion, as well as diffusion thermal conductivity can be neglected, since the volume of the reaction mixture does not vary by more than 10%, and it is highly diluted with inert gas N₂; molecular weights of components and, thus, their diffusion coefficients differ insignificantly [7].The temperature of the catalyst in the bed of PGM-gauzes is assumed to be constant and is determined by the adiabatic heating of the coming reaction mixture. On this basis, to describe the process, a model of plug-flow for the gas phase is accepted with the use of material balance equations for each component.

The material balance equation of the process occurring at a significant influence of external mass transfer to the i-component is as follows:

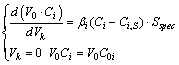, (7)

where i = 1, 2, 3, 4, 5, 6 – the following components respectively: NH₃, O₂, NO, H₂O, N₂O, N₂; V₀ × C_i – molar amount of the i-component in the catalyst layer; V_k – the volume of the catalyst layer; C_i, C_i,S – the current concentration of i-component in the flow of reactants and on the surface respectively; C_0i – the initial concentration rate of ammonia and oxygen in the reaction mixture; b – mass transfer coefficient between the catalyst surface and the flow of the reaction mixture; S_spec – specific geometric surface of catalyst PGM-gauzes per unit of volume.

For ammonia and oxygen the equation (8) has the following form:

, (8)

where i = 1, 2; x_i – the degree of conversion of ammonia and oxygen, mole fraction; y_0i – the initial mole fraction of ammonia in the mixture; y_i, y_iS – the current mole fraction of ammonia and oxygen in the volume and on the surface of the catalyst; t – the contact time, s; ; – volumetric flow rate of the gas mixture under normal conditions (T = 273 K, p = 0.098 MPa).

Similar equations were obtained for all components in the reaction mixture. A mathematical description of ammonia oxidation process in the catalyst layer has the following form:

(9)

with boundary conditions t = 0, x_i =0, x_k = 0; where = 3, 4, 5, 6; x_к – mole number of NO, H₂O, N₂O, N₂ formed from one mole of ammonia.

The mole fraction of nitrogen y₆ was calculated according to the equation:

. (10)

The current concentration of components in the mixture was calculated according to the mole fractions by the formulas:

, (11)

where i = 1, 2;

, (12)

where = 3, 4, 5, 6; N – the current number of moles of the reaction mixture, which is equal to the current sum of the moles of each component.

Concentration of substances on the catalyst surface was determined according to the following equations:

, , (13)

where i = 1, 2, 3, 4, 5, 6; T₀ – temperature of the mixture in the gas volume, K; T_S – the catalyst surface temperature, К; r_j – the reaction rate on the j-route (reactions 1–4); – the thermal effect of the reaction on the j-route; – the coefficient of heat transfer from the gauzes to the gas stream, kJ /(m²·s·К).

The system of equations (7–13) is the mathematical model of external diffusion processes of ammonia oxidation on catalyst PGM-gauzes.

The degree of NH₃ oxidation on PGM-catalysts was calculated according to the developed mathematical model. For calculating this process it is necessary to know the coefficients of heat and mass transfer from the gas flow to the catalyst, as well as the physical and chemical properties of the mixture, depending on the temperature, pressure and composition of the mixture.

By solving the inverse problem of chemical kinetics, using the experimental data, we determined reactions rates constants connected with the formation of NO (k₁), N₂O (k₂), N₂ (k ₃) and N₂, resulting from the nitrogen (ІІ) oxide decomposition (k₄), and the concentrations of the substances on the catalyst surface [12–14]. The comparison of calculated and experimental conversion coefficients shows good agreement, the difference is not more than 1–3%.

Conclusions. A mathematical model of the oxidation process of NH₃, considering the physical and chemical properties of the ammonia-air mixture and nitrous gas has been developed. The rate constants and their temperature dependence have been determined. This will allow to determine the optimal process conditions of NH₃ oxidation on the PGM-catalyst at different pressures in a wide range of process parameters, as well as to determined the amount of nitrogen oxides N₂O formed. On the basis of the developed model, a program for calculating the NH₃ oxidation reactor using PGM-catalysts of different geometric profile has been created. During the operation process, the volume and the surface of the catalyst are changed. Thus the mathematical model for the rates of ammonia oxidation steps per unit mass of PGM-catalyst has been developed.

REFERENCES

[1] Savenkov А.S.: Catalyticheskie svoistva poverhnosti platiny v reakcii оkislenia amiaka i matematicheskoe modelirovanie processa [in:] A. Loboiko (Ed.), Catalyticheskie i massoobmenye processy pod davleniem v technologii neorganicheskih veshchestv, Kharkov, Osnova 1993, 46-63.

[2] Savenkov А.S., Beskov V.S.: Кinetica processa okislenia ammiaka na platinovom katalizatore pod davleniem [in:] V.I.Atroshchenko (Ed.), Кinetica geterogenno-kataliticheskih processov pod davleniem, Kharkov, Vishcha shkola 1974, 67–83.

[3] Vyatkin Ju.L., Savenkov А.S., Beskov V.S.: Khimicheskaja Promishlennost, 1979, 10, 618.

[4] Beskov V.S., Vyatkin Ju.L., Savenkov А.S.: Teoreticheskie Osnovy Khimicheskoi Tehnonologii, 1980, 14, 442.

[5] Beskov V.S., Кusnkov А.P., Novikov E.А. et al.: Khimicheskaja Promyshlennost, 1977, 9, 691.

[6] Savenkov А.S., Beskov V.S., Vyatkin Ju.L.: Proceed. 10^th Annual Conference "Сhemreactor-10", Ukraine, Kharkov, 1992,  339.

[7] Beskov V.S., Brushtein Е.А., Golovnia Е.В., Vanchurin V.I.: Catalysis in Industry, 2008, 2, 31.

[8] Pérez-Ramírez J.: Applied Catalysis B: Environmental, 2003, 44, 117.

[9] Cybulski A., Moulijn J.A., Stankiewicz A. Novel. Concepts in Catalysis and Chemical Reactors. – WILEY-VCH, 2010, 372 p.

[10] D.A. Hickman , L.D. Schmidt: Ind. Eng. Chem. Res., 1991, 30(1), 50.

[11] Vargaftik N.B. Spravochnik po teplophysicheskim svoistvam gasov i zhidkostei, Nauka, Moscow, 1972.

[12] Bliznjuk О.N., Savenkov А.S., Masalitina N.Yu., Ogurtsov A.N.: Visnyk NTU "KPI", 2010, 13, 8.

[13] Bliznjuk О.N., Savenkov А.S., Masalitina N.Yu., Ogurtsov A.N.: Khimichna Promyshlovist Ukraine, 2010, 3(98), 3.

[14] Bliznjuk О.N., Savenkov А.S., Ogurtsov A.N., Chlopitskii A.A.: Voprosy Khimii i Khimichnoi technologii, 2012, 6, 92.