Пиль Э.А.

Заслуженный деятель науки и образования РАЕ, д.т.н., профессор.

ВЛИЯНИЕ ТРЕХ ПЕРЕМЕННЫХ НА РАСЧЕТ ВАЛОВОГО ВНУТРЕННЕГО ПРОДУКТА

Ранее автор в своих статьях показал, как влияют изменения трех переменных на расчет валового внутреннего продукта, при этом все переменные изменялись по-разному. В предлагаемой ниже статье рассматривается вопрос, где одна переменная изменяется, а две других, увеличивались или уменьшались одинаково, либо все три переменные изменялись одинаково.

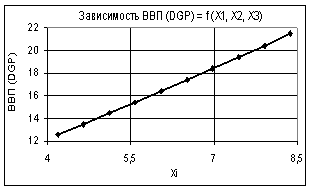
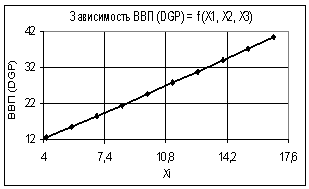
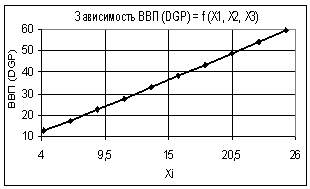
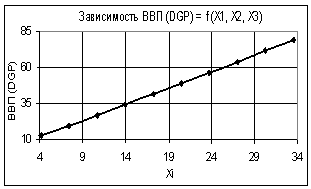
Так на рис. 1 показана зависимость ВВП (GDP) = f(Х1, Х2, Х3) при следующих значениях переменных: Х1 = 1…2, Х2 = Х3 = 1. Как видно из данного графика, построенная зависимость изменяется по линейному закону. Проведенный корреляционно-регрессионный анализ показал, что коэффициент корреляции R² = 0,9998 имеет значение близкое к единице. То есть, полученное линейное уравнение позволяет нам рассчитывать ВВП (GDP) по упрощенной формуле с достаточно высокой точностью. Здесь среднеквадратическая ошибка составила значение 0,055.

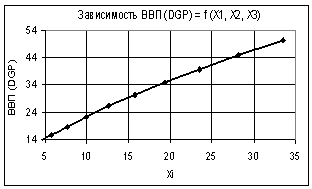
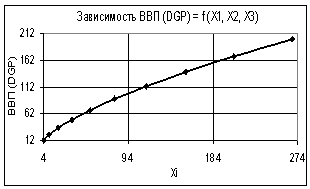
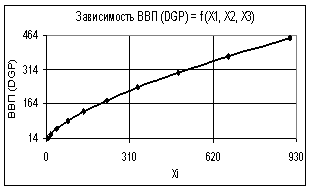
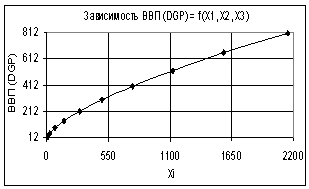
На втором рисунке показана аналогичная зависимость, но только здесь все переменные увеличиваются одинаково. Здесь построенная зависимость ВВП (GDP) = f(Х1, Х2, Х3) изменяется уже по степенному закону, при этом коэффициент корреляции R² = 1,0, что также позволяет нам говорить о возможном упрощенном варианте расчета ВВП (GDP) с большой точностью. В данном примере среднеквадратическая ошибка составила значение 0,000.

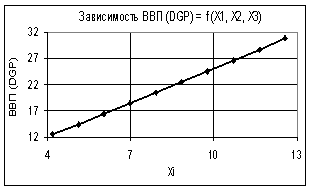
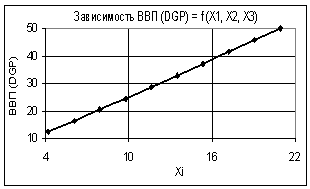
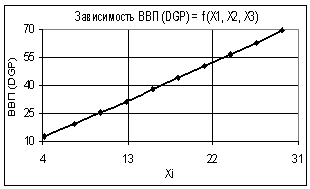
Из следующего рис. 3 видно, что при значениях переменных: Х1 = 1…3 и Х2 = Х3 = 1 построенная зависимость также представляет собой линейную функцию с высоким коэффициентом корреляции R2 = 0,9998. Среднеквадратическая ошибка получилась 0,268.

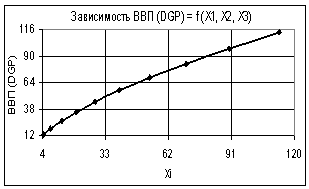
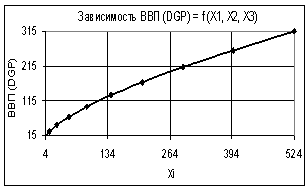
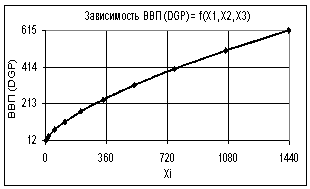
Если же изменяются все переменные Х1 = Х2 = Х3 = 1…3, то в этом случае мы опять получаем степенную зависимость со следующем коэффициентом корреляции R² = 1,0 (рис. 4). Среднеквадратическая ошибка здесь составила 0,000.

Рис. 1. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = 1…2, Х2 = Х3 = 1		Рис. 2. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = Х2 = Х3 = 1…2
Рис. 3. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = 1…3, Х2 = Х3 = 1	Рис. 4. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = Х2 = Х3 = 1…3

На двух рисунках 5 и 6 представлены две зависимости изменения переменных при следующих их значениях: Х1 = 1…4, Х2 = Х3 = 1 и Х1 = Х2 = Х3 = 1…4 соответственно. Здесь также как и выше были получена линейная зависимость для рис. 5 и степенная для рис. 6. В этом случае коэффициенты корреляции были R² = 0,9998 и R² = 1,0. Среднеквадратические же ошибки здесь были 0,575 и 0,000 соответственно.

На следующих двух рисунках 7 и 8 показаны аналогичные зависимости, но только для Х1 = 1…5, Х2 = Х3 = 1 и Х1 = Х2 = Х3 = 1…5 соответственно. В этом случае были получены также высокие коэффициенты корреляции R² = 0,9998 и R² = 1,0. Подсчеты среднеквадратических ошибок показали следующие значения 0,926 и 0,000 соответственно.

Рис. 5. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = 1…4, Х2 = Х3 = 1		Рис. 6. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = Х2 = Х3 = 1…4
Рис. 7. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = 1…5, Х2 = Х3 = 1	Рис. 8. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = Х2 = Х3 = 1…5
Рис. 9. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = 1…6, Х2 = Х3 = 1			Рис. 10. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = Х2 = Х3 = 1…6

На рисунках 9 и 10 показаны аналогичные зависимости, но только для Х1 = 1…6, Х2 = Х3 = 1 и Х1 = Х2 = Х3 = 1…6 соответственно. Здесь были получены следующие высокие коэффициенты корреляции R² = 0,9998 и R² = 1,0. Подсчеты среднеквадратических ошибок показали следующие значения 1,295 и 0,000 соответственно.

Рисунки 11 и 12 дают наглядное представление, как изменяются зависимости для Х1 = 1…7, Х2 = Х3 = 1 и Х1 = Х2 = Х3 = 1…7 соответственно. В данном примере были получены следующие коэффициенты корреляции R² = 0,9998 и R² = 1,0. Подсчеты среднеквадратических ошибок показали следующие значения 1,926 и 0,000 соответственно.

Рис. 11. Зависимость ВВП (GDP) =f(Х1, Х2, Х3) Х1 = 1…7, Х2 = Х3 = 1	Рис. 12. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = Х2 = Х3 = 1…7
Рис. 13. Зависимость ВВП (GDP) =f(Х1, Х2, Х3) Х1 = 1…8, Х2 = Х3 = 1		Рис. 14. Зависимость ВВП (GDP) = f(Х1, Х2, Х3) Х1 = Х2 = Х3 = 1…8

На последних двух рисунках 13 и 14 представлены две зависимости для Х1 = 1…8, Х2 = Х3 = 1 и Х1 = Х2 = Х3 = 1…8 соответственно. В данных примерах были получены следующие коэффициенты корреляции R² = 0,9999 и R² = 1,0. Подсчеты среднеквадратических ошибок показали следующие значения 2,037 и 0,000 соответственно.

Здесь следует отметить, что у всех полученных степенных уравнений значения коэффициента и степени были одинаковыми.