Сламкулова М. Б.АбдикуловаЕ.Е

Таразский гогсударственный университет, Казахстан

Проектные решения по технологии разработки программ синтеза реалистичных трехмерных изображений

Метод плавающего горизонта. Здесь, в отличие от предыдущего метода, грани выводятся в последовательности от ближних к самым дальним. На каждом шаге границы граней образуют две ломаные линии - верхний горизонт и нижний горизонт. В течение вывода каждой новой грани рисуется только то, что выше верхнего горизонта, и то, что ниже нижнего горизонта. Соответственно, каждая новая грань поднимает верхний и опускает нижний горизонты. Этот метод часто используют для показа поверхностей, которые описываются функциями z=f(x,y).

В общем виде метод выглядет следующим образом.

Пусть надо построить график функции двух переменных Z=f(x, y), в виде сетки координатных осей.

При параллельном проектировании проекций вертикальной линии является вертикальная линия.

Любая точка P(x, y, z) переходит в точку [(p_,e₁), (p, e2)] на плоскости экрана, где

e₁= (cosφ, sinφ, 0)

e₂= (sinφ, sinq, - cosφ sinq, cosq), а направление проектирования:

e₃= (sinφ cosq, - cosφ - cosq, sinq) (22)

где φє[0, 2π], qє[-π/2, π/2] - углы подобраны так, чтобы плоскость у=у₁ была ближе к экранной плоскости, чем у=у₂, т.е. у₁<у₂.

Из этого следует, что линия Z=f(x, y_j), не закрывает линию Z=f(x, y_i).

Тогда возможен алгоритм, когда линии рисуются в порядке удаления (возрастания у) и при рисовании очередной линии рисуется только та ее часть, которая не закрывается ранее нарисованной.

Для определения частей линий Z=f(x, y_к), которые не закрываются ранее нарисованными, вводятся линии горизонта.

Пусть проекцией линии Z=f(x, y_к) на плоскость экрана является линия у=у_к(х), где (х, у) – это координаты на экране. Тогда линии горизонта определяются как:

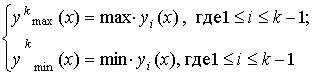(23)

На экране рисуются только те части линии у=у^к(х), которые выше у^к_max(х) или ниже у^к_min(х).

Проще всего этот метод реализовать с помощью модифицированного растрового алгоритма Брезенхейма, который перед выводом очередного пикселя сравнивает его ординату с верхней и нижней линией (массивы ординат).

Аналогичным методом можно воспользоваться при построении объемных предметов. Только в этом случае изображение выводится по мере удаления от экранной плоскости, а по мере – приближения, т.е. начиная с дальних граней, и, заканчивая ближними, которые будут закрывать собой невидимые части более дальних граней.

Для определения порядка вывода граней считают, что грань, лежащая в полосе не может закрыть грань из полосы

Метод Z-буфера.

Здесь используется специальный дополнительный массив (буфер), в который записывается координата Z для каждого пиксела растра изображения. Координата Z означает расстояние соответствующей точки объекта до плоскости проецирования - это может быть, например, видовая координата Z (ось Z располагается перпендикулярно плоскости проецирования).

Рассмотрим алгоритм рисования объектов в соответствии с этим методом. Пусть, чем ближе точка в пространстве к плоскости проецирования, тем больше значение Z. Тогда сначала Z-буфер заполняется минимальными значениями. Потом начинается вывод всех объемов. Причем, не имеет значения порядок вывода объектов. Для каждого объекта выводятся все го пикселы в любом порядке. Во время вывода каждого пиксела по его координатам (X,Y) находится текущее значение Z в Z-буфе_Ре. Если рисуемый пиксел имеет большее значение Z, чем значение в Z-буфере, то этот пиксел действительно рисуется, а его Z-координата записывается в Z-буфер. Таким образом, после рисования всех пикселов всех объектов растровое изображение будет состоять из пикселов, которые соответствуют точкам объектов с наибольшими значениями координат Z, то есть видимые точки являются ближайшими к нам.

Укажем некоторые проблемы использования метода Z-буфера.

1. Необходимость выделения дополнительной памяти. Для Z-буфера необходима память объем которой соответствует размерам растра изображения и точности чтения координаты Z. Используют обычно 32, 24 или 16 битов на один пиксел Z-буфера. Например для Z-буфера 1024x768x32 нужно 3 Мбайта. Сейчас такие затраты памяти не считаются существенными. Если объем памяти _ критичен, то кадровый и Z-буфер разделяют на фрагменты (тайлы) и выполняют визуализацию для любого фрагмента отдельно. Файловая организация Z-буфера может использоваться также и для повышения скорости визуализации.

2. Полная инициализация Z-буфера (запись "самых дальних" значений) перед началом вывода того кадра уменьшает скорость анимации. Тем не менее, часто используется такой прием - инициализировать Z-буфер один раз для пары кадров. Это возможно, если разделить полный диапазон значений Z пополам. Например, если полный диапазон значений от 0 до 1, то в первом кадре работать со значениями Z, смещенными в интервал от 1 до 0.5 (дальняя половина), а в следующем кадре - от 0.5 до 0 (ближняя половина). Однако за повышение скорости здесь приходится платить точностью вычисления глубины -она уменьшается вдвое.

3. Большое количество лишних операций. Поскольку видимость устанавливается на уровне пикселов, то в цикле выполняются лишние операции для тех полигонов, которые полностью невидимы. Такие полигоны желательно отсекать до цикла вывода. Для ускорения вывода насыщенных сцен, содержащих миллионы полигонов, известны модификации метода, например, иерархический Z-буфер, в котором используется пирамида 2-х буферов разной разрешающей способности.

4. Проблемы с выводом полупрозрачных объектов.

5. Использовать в качестве расстояния координату 2 нельзя при углах обзора 180 градусов и больше. Для цилиндрических и сферических проекций лучше использовать радиальное расстояние от текущей точки объекта до точки схода лучей проецирования.

Несмотря на кажущуюся простоту, эта задача является достаточно сложной.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1 Авдеева С.М., Куров А.В. Алгоритмы трехмерной машинной графики: учебное пособие. – М.: Издательство МГТУ им. Н.Э.Баумана, 1996. – 60 с., ил.

2 Никулин Е. А. Компьютерная геометрия и алгоритмы машинной графики. СПб.: БХВ-Петербург, 2003. – 560с.: ил.

3 Авдеева С.М., Куров А.В. Алгоритмы трехмерной машинной графики: Учебное пособие. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1996. – 60 с.: ил.

4 Иванов В.П., Батраков А.С. Синтез изображений объектов сложной формы методом трассирования лучей // Программирование.-1989.2.-С. 70-75.