Магистрант Заденова Т.А. , научный руководитель Айткожа Ж.Ж.

(Л.Н. Гумилев атындағы Еуразия ұлттық университеті)

Бейнелерді өңдеуде ақырлы өрістердегі Хаар типті вейлвет-тәрізді түрлендірулері қолдану басымдығы

Бүгінгі күні бейнелерді өңдеу, сығу, сақтау жүйелері көптеп қолданылуда. Жылдан жылға бейнелердің жадыда алатын орнын азайту мақсатында көлемін кішірейту, алайда сапасын сақтап қалу арқылы сығу жүйелерінің жаңа түрлері шығып жатыр. Бұл жүйелердің әрқайсысы әр түрлі әдіс тәсілдермен және әр түрлі форматтар үшін орындаған. Бұл тақырыптың өзектілігін ескере отырып, бейнелерді сығу, қалпына келтіруді орындаудың тағы бір әдісі ақырлы тақ өрістегі Хаар типті вейлвет түрлендіру арқылы орындап артықшылықтары мен басымдылықтарын зерттеп көрдім.

Мақалада ақырғы өрістердегі Хаар типті вейлвет-тәрізді түрлендірулердің (ХТВТТ) теориясы көрсетілген. Хаар типті вейлвет-тәрізді түрлендірулері түрлендіру матрицасының жалпы түрдегі матрицаға ауыстыру арқылы Хаардың вейлвет түрлендірілулерінен (ХВТ) пайда болады. Соңғы өріс арифметикасы, бұл түрлендірулердің тура айналымды отбасылық түрін айналдыру қателерінсіз реализациялауға мүмкіндік береді. Бұл түрлендірулердің абсолютті нақтылығы және бірреттік қолданылу кезінде сызықтық күрделілігі, олардың аудио, мәтін, бейнелерді жоғалтусыз өңдеуді тиімді қолдануын болжауға мүмкіндік береді. Бұл түрлендірулерді мәліметтерді қысу, және бейнелерді анықтау автоматтандырылған жүйелерінде белгілерді құрастыруға қолдану ұсынылады.

Бұл жұмыстың мақсаты – жай ақырғы өрістерде вейлвет-тәрізді түрлендірулердің теориясын ұсыну. Кез-келген ақпараттық жүйенің жұмыс сапасын бағалау критерийлері субъективті. Алайда, оның сапасын бағалауда екі негізгі аспектті бөліп көрсетуге болады:

1) Ақпаратты өңдеу, сақтау, қабылдау, жіберу сапасы;

2) Ақпараттың адаммен қабылдану сапасы.

Бұл сапаны бағалау аспектілері бірдей емес. Егер ақпаратты соңғы қабылдаушы адам болса, жүйеге адамның ақпаратты қабылдауына ыңғайлы интерфейс қосу қажет. Ақпаратты жіберу, қабылдау, сақтау және өңдеу жоғалтулармен және жоғалтуларсыз жүзеге асуы мүмкін. Егер адам өз сезім органдары арқылы сезбесе, жоғалтулардың болу, болмауы адамға бәрібір. Жүйенің адам қатысысыз автоматты жұмысы кезінде, кез-келген жоғалтуларды минимумға әкелу немесе олардың кейбіреуін мүлдем алып тастау өте маңызды. Жоғалтулардың негізгі екі түрін бөліп көрсетуге болады:

1) Жөнелту каналдары және жады элементтерімен шартталған жоғалтулар;

2) Өңдеу алгоритмдерінің жетілмегендігі мен табиғатынан туындаған жоғалтулар.

Осыған орай, ақпараттың жадыдағы сақталу, есептік өңдеу, әртүрлі физикалық табиғатқа ие байланыс каналдары арқылы беру бойынша техникалық мәселелер актуальдығы өсіп келеді.

Ақпаратты сақтау, жөнелту және өңдеу сигнал ұғымымен тығыз байланысты. Матиматикалық тұрғыдан қарағанда сигнал – бір немесе бірнеше айнымалылардың бірлік немесе көптік функциясы. Бір айнымалының бірлік сигналдарының арасында, анықталу облысына және мүмкін мәндер аймағына байланысты, аналогтік (R→R), дискреттік (Z→R), кванттық (R→Z) және цифрлық (Z→Z) сигналдар бар. Аралас түрлі сигналдар да болуы мүмкін. Компьютер ресурстарының шектеулігіне байланысты, көптеген бағдарламаларда цифрлік сигнал, кейбір M,N>1 натурал сандарында Z_M→Z_N көрсетеді. Есептеу тұрғысынан қарағанда, f: Z_M→Z_N функциясы әртүрлі тәсілдермен пайдаланылуы мүмкін:

1) Арифметикада сипаттау өрістері 0 (Q немесе R)

2) Арифметикада Z_M,N дөңгелектері – құрама сан

3) Арифметикада Z_P=GF (P), P өрістері – жай сан

4) Арифметикада GF (P^K), P өрістері – жай сан,K>1 – натурал сан

5) Аса қиын алгебралық құрылымдар арифметикасында

Бірінші әдіс дөңгелектеу қателіктеріне ие (R қолданған кезде) немесе жадының көлемін үлкейтуді талап етеді (Q қолданған кезде). Екінші әдіс «кәдімгі» арифметикамен нашар келісіледі, ол физикалық нәтижелерді сәйкес түсіндіруге мүмкіндік бермейді. Үшінші және төртінші әдістерде бірінші екеуінің кемшіліктері жоқ. Алайда, екінші, үшінші, төртінші әдістер физикалық қаралымдардың шынайы мәндерін кейде көрсетпейді.

1 жұмыстарда әртүрлі вейлветтердің қолданылуы және теориясымен танысуға болады. 3,4 жұмыстарда вейлветтердің бейнелер мен сигналдардын өңдеуін толық көруге болады. 5,6 кітаптардан Галуа өрістері және Галуа өрістеріндегі тура есептеу алгоритмдері жайлы толық ақпарат алуға болады.7 жұмыс вейлветтер теориясының қазіргі жағдайы жайлы толық мағлұмат береді. 2 мақалалар вейлветтердің бейнелерді қысу бойынша қолдану перспективаларын көрсетеді. Хаар базисіндегі вейлвет-түрлендірулер N=2ⁿ – өлшемді сызықтық кеңістіктер үшін кез-келген сипаттамалы, ерікті өрістер қатынасы (1),(2) анықталады.

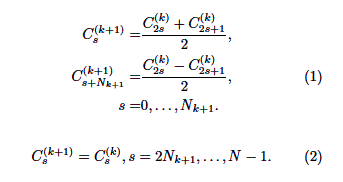
Еркін өрісте Хаар базисындағы вейлвет түрлендіру тәрізді түрлендіру

Хаар базисіндегі вейлвет-түрлендіру жоғарыжиілікті және төменжиілікті есептеулермен байланысты, екі пайдалы қасиетке ие:

1) Егер екі элемент бірдей болса, түрлендірудің нәтижелерінің біреуі кез келгеніне тең;

2) Егер екі элемент бірдей болса, түрлендірудің екінші результаты нөлге тең.

Бұл қасиеттер бейнелерді өңдеу кезінде өте пайдалы. Бейнелер көбінде бірдей немесе ұқсас көптеген пикселдер кодына ие. Сондықтан, бейнелердің пиксельдерінің көбі бірге айналып кеткен, немесе модулі бойынша аз болғандықтан, ондай бейнелерді қазіргіге қарағанда кішірек кодтар түрінде көсетуге болады, яғни қысу. (1) түрлендіруінде жартысомма және жарты әртүрлікті аталған қасиеттерге ие кез келген түрлендірумен алмастырайық. Нәтижесінде (3), (4) түрлендірулерін аламыз. (3), (4) амалдарымен анықталатын түрлендірулерді Хаар вейлвет түрлендіруі тәрізді түрлендіру деп атаймыз.

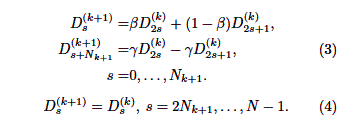
(3), (4) түрлендірулері еркін өрістер элементтерімен жүргізілуі мүмкін.

Ақырлы тақ өрістегі Хаара базисіндегі вейлвет түрлендіру тәрізді түрлендіру

GF (P) жай өрісі өзін жай санның модулі бойынша алып тастау сақиналар классы болады, ал GF (P^K) өрісінің кеңейтімі – GF (P) –дан алынбайтын полином модулі бойынша сақина полиномдар факторы. Нормаланған алынбайтын полиномдар саны К дәрежесінде GF (P) [5] дан мынаған тең:

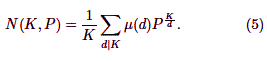
Мұнда µ (•) – Сандар теориясынан Мебиус функциясы. Бұл алынбайтын полиномдардың кез-келгени арифметикада Галуа өрісін есаептеуге қолданылуы мүмкін. Алайда, К дәрежесінде GF (P)нормаланған алынбайтын примитивті полиномдар негізінде есептелімдер жақсырақ болып келеді. Есептеулер өрістің мультипликативті тобының қасиеттері арқылы жеңілдетіледі. Нормаланған, алынбайтын примитивті полиномдар саны мынаған тең:

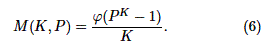
Мұнда φ (•) – сандар теориясынан Эйлер функциясы. Кез-келген мәлімтеттерді өңдеу үшінтәжірибелік бағдарламаларда 2GF (2^K), K>1 сипатындағы ақырғы өрістерді қолданған жөн. Ол бәрінен бұрын компьютерлі к арифметикамен байланысты. Мысалы (7) формулалары - алынбайтын полиномдар үшін амал. Оларды GF (2^K) , K=4,8,16,24,32 Галуа өрісі кеңейтілімінде есептеу үшін қолдануға болады.

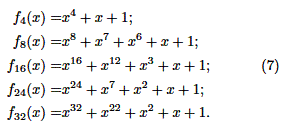
Мұндай к-лар үшін GF (2^K) өрісінің элементі сақтау үшін байт, сөз, 3 байт, жартыбайт, екі еселенген сөз талап етеді.

Қорытындылар

Көрсетілген зерттеуді қорытындылай келе келесідей нәтижеге келуге болады.

1) ХВТ матрицасының құрылымына талаптарды нашарлату, бұл түрлендірулердің класстарын кеңейтеді. Шығатын түрлендірулер классын ХТВТТ деп атауға болады.

2) ХТВТТ-ның үлкен екі түрін бөліп көрсетуге болады – анықталмаған матрицилиармен пайда болған немесе симметриялық анықталмаған матрицилиармен пайда болға. Екінші түрі бірнші түрдің түрасты түрі болады.

3) ХТВТТ GF (2) басқа кез-келген типті, кез-келген өрісте пайдаланылуы мүмкін.

4) Ақырғы өрістегі ХТВТТ өзара біртекті бейнелену векторы н осы өрісте дөңгелектеу қателіктерісіз жүзеге асырады.

5) Мәліметтрді компьютерлік өңдеуде бағдарламалар ретінде GF(2K), K > 1 өрісінен ХТВТТ көп қызығушылық туғыза алады.

Айтылған нәтижелер, ақырғы тақ өрістегі ХТВТТ дөңгелектеу қателігінсіз орындайтын математикалық объект ретінде да, мультимедиялық ақпаратты өңдеу инструменті ретінде де қызығушылық туғызады деп қорытындылауға болады.

Пайдаланылған әдебиеттер тізімі

1) Чуи Ч. Введение в вейвлеты. - Москва: Мир,2001. - 412 б.

2) Яковлев А.Н. Введение в вейвлет-преобразования._Новосибирск: НГТУ, 2003. - 104 б.

3) Столниц Э.Р., ДеРоуз Т., Салезин Д. Вейвлеты в компьютерной графике._Ижевск: НИЦ Регулярная и хаотическая динамика, 2002. -272 б.

4) Малла С. Вэйвлеты в обработке сигналов. - Москва: Мир, 2005. -671 б.

5) Лидл Р., Нидеррайтер Г. Конечные поля.Москва: Мир, 1988. -820 б.

6) Блейхут Р. Быстрые алгоритмы цифровой. -Москва: Мир, 1989. - 448 с.

7) Fekri F., Mersereau R.M., Schafer R.W. Theory of wavelet transform over finite fields // Proceedings of the Acoustics, Speech, and Signal Processing (ICASSP), 1999. -Vol. 03. -Pp. 1213–1216.