Ералиева Б.Ш.

Таразский Государственный Университет им. М.Х. Дулати

г.Тараз, Казахстан

СЫЗЫҚТЫ ЕМЕС ПРОГРАММАЛАУ ӘДІСТЕРІ.

СЫЗЫҚТЫ ЕМЕС ПРОГРАММАЛАУ ЕСЕПТЕРІН БАҒДАРЛАМАДА ШЕШУІНІҢ ТИІМДІДІГІ.

Сызықты емес программалау есебі класы сызықты программалау есебі класынан ауқымдырақ. Сызықтық деп есептелінетің практикалық есептерді толық зерттеу нәтижесі олардың шын мәнінде сызықтық емес екендігін көрсетеді. Сызықты программалау есептерді шешімдерінін тиімдісің табу мәселесі туындайды. Тіпті шешім алынған облыс дөңес облыс болса, онда есептер қатарында мақсаттық функция бірнеше локалді экстремумға ғана ие болуы мүмкін. Көптеген есептеу әдістерінің көмегімен локалді оптимум нүктесін табуға болады, бірақ, ол глобалдік (абсолюттік) оптимум нүктесі болатын, болмайтынын анықтау мүмкін емес. Егер сызықтық программалау есептерінде шешімнің экстремум нүктесі көпжақтың төбесі болса, онда сызықты емес программалау есептерінде көпжақтың төбесінде, қабырғасында немесе облыстың ішінде жатуы мүмкін.

Егер есеп сызықты емес шектеулі болса, онда шешім алынған облыс дөңес болмайды, сондай-ақ глобалдік оптимумнан басқа локалдік оптимум нүктесі табылуы да мүмкін.

Нақты объектілерді немесе технологиялық процесстерді жобалау есептерінде математикалық моделдер нақты ішінде болатын физикалық яғни сызықты емес процесстерді көрсету қажет. Сол объекттердің немесе процесстердің айнымалылары физикалық сызықты емес зандармен өз – ара байланысады, ол массаны немесе энергияны сақтау зандары. Олар осы объектті немесе процессті физикалық өткізілімділігін қамтамасыз ететін шекті диапазондармен шектелген. Нәтижесінде ғылыми-зерттеу жобада және жобалау есептерінде кездесетін көп математикалық программалау есептері-ол сызықты емес программалау есептері (СЕП).

Сызықты емес программалау әдістердің ешқайсы әмбебап болып саналмайды. Әрбір нақты жағдайда қолданатын әдістін шешілетің есептің ерекшеліктеріне бейімделу қажет.

Сызықты емес программалау есебінін жалпы түрі:

Z=ƒ (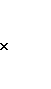, , 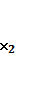....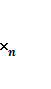)→max (min)

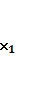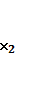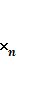(, , ....)≤, i=1,2,…, m,

Нысаналы функцияға және айнымалылардың шектеулеріне сызықтық талаптары жоқ.

Классикалық тиімдеу әдістеріне жататың сызықты емес есептер класстары болады. Оларға орындалатың шарттар:

· Шектеулер арасында теңсіздіктер жоқ;

· Айнымалылар терістіктер шарттары міндетті емес;

· Дискреттік айнымалылар жоқ;

· m, φ_i., f үздіксіз және екінші реттік дербес туынды болады

Сызықты емес және математикалық программалау есебі келесі түрде беріледі:

Айнымалыларды табу (, , 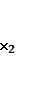....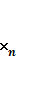), шарттарға қанағаттандырылады (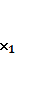, , 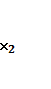....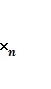)=, i=1,2,…, m және функцияны максимумға (минимум) айналдырады z= ƒ (, , ....),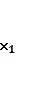

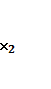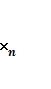Сызықты емес программалау есептерінде f(x) нысаналы функцияны минималдайтын көп өлшемді айнымалынын мәнін х=( ) табу қажет, сол сәтте х айнымалыларына тенсіздіктер түрінде (x)≤0 i=1,2,…,m, шектеулер қойылған, ал айнымалылар, яғни х ветордың компоненттері теріс емес ≥0 болады.

Кейде есептер тұжырымында шектеулер теңсіздіктердің қарама-қарсы таңбалары алып жатады. Сонымен қатар егер (x)≥0 , онда (x)≤0, осы жағдайларда есептерді бір таңбалы теңсіздіктерге келтіруге болады. Егер кейбір шектеулер тең таңбалы есептерге кірсе, мысалы ø(x)=0, онда оларды ø(x)≤0, -ø(x)≤0 қос теңсіздіктер түрінде көрсетуге болады, осылайша мәселенің типтік тұжырымын сақтау.

Есеп сызықты емес програмалау есебы деп аталы, егер оның математикалық моделі

келесі түрде жазылады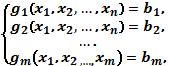

ƒ(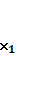, , 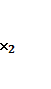....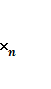)→max (min), осында немесе ƒ арасында сызықты емес функциялары бар.

Сызықты программалау есептеріне қарағанда сызықты емес программалау есептер шешім үшін біртұтас әдіс болмайды.

Сызықты емес программалау есептерін Excelқұралдарымен шешу сызықты программалаудан айырмашылығы келесіде:

· бастапқы нүктеде нысаналы функция нөлге тең болмайтындай айнымалылардын бастапқы мәндерін белгілеу керек, ƒ (, ,…, ,);

· Поиск решения диалогты терезеде Параметры режимінде Линейная модель деп еңгізбейміз.

Сызықты емес программалау есептері Microsoft Excel-де сызықты программалау есептер сияқты шешіледі, те қана "Параметры поиска решения" терезесінде "Линейная модель" жалаушаны алу керек және қажет болса "Неотрицательные значения".

Мысал 1.

Microsoft Excel –де келесі сызықты емес программалау есебін шешу:

Табу ƒ=4+ + 8+ →min шарт бойынша +=180

Бұл моделде шектеулер жүйесі бір сызықты теңдеуден және сызықты емес нысаналы функциядан тұрады.

Шешім

1. Жұмыс парағында ұяшықтарды қажетті айнымалылармен, нысаналы функциямен және шектеулермен толтыру:

2. "Параметры поиска решения" терезесінде "Линейная модель"(өйткені шешілетін есеп сызықты емес программалау есебі болып табылады) және "Неотрицательные значения" жалаушаны алып тастау.

3. "Выполнить" батырманы басудан кейін жауап пайда болады: шығатын, не нысаналы функцияның ең төменгі мәні 17278-ге тең және x₁ = 91 және x₂ = 89 нүктелерде жетеді.

Мысал 2:

Берілген сызықты емес есептің математиалық қойылымы (f(x) нысаналы функцияның және шектеулер – теңдіктер) келесі қадамдарды орындау:

Лагранждың көбейткіштердің әдісімен функциялардың барлық шартты экстремум табу керек және олардың арасында глобалді минимум (максимум) таңдау керек;

Excel кестелік процессорынде шешімнің нәтижесін тексеру;

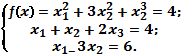
Шешім Лагранждың көбейткіштердің әдісі

1. Лагранж қосымша функциясын құру:

F(x, λ)=f(x)+ (x)

Осы есепке:

F(x, λ)=+3++(++2-4)+(-3-6)

2. Осы функцияны дифференциалдау , және бойынша теңдеу жүйесін жазу:

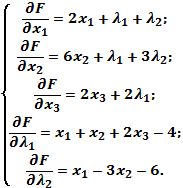
3. Көп айнымалылардың эстремум функциясын табу үшін оның барлық дербес туындыларын нөлге теңестіру керек және табылған теңдеу жүйесің шешу керек.

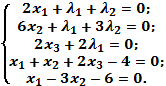
4. Шешімнің нәтижесі:

=2,25, =-1,25, = 1,5, =-1,5 және =-3, F=12

Excel кестелік процессорынде шешімі.

Excel процессор көмегімен есепті шешу келесі нәтижелерді береді:

х1	х2	x3
2,25	-1,25	1,50
Нысаналы функция	12,00
Шектеулер	4,00	=	4
6,00	=	6

Есепті екі әдіспен шешу бірдей нәтиже берді.

Әдебиет тізмі

1. Таха, Хемди А. Введение в исследование операций. М.: Издател. дом «Вильяме», 2005, 912 с.

2. Соловьев В. И. Учебное пособие. Методы оптимальных решений. М.: Финансовый университет, 2012. 364 с.

3. Емельянов Е.Г. Основы сетевого планирования. СПб.: Изд-во СПГУЭФ, 2010, – 16 с