Д.т.н, профессор Христофоров Б.Д.
Институт динамики геосфер РАН, Москва

Моделирование воздействия гроз на наземные объекты и низколетящие летательные аппараты с применением разряда, лазерного излучения и взрыва.

Введение

Согласно [1], ежегодно на Земле происходит свыше 30 млрд. грозовых разрядов, которые обычно возникают внутри грозовых облаков, между ними и реже между облаком и землей или ионосферой. В отдельном грозовом облаке электрическая энергия может достигать 10¹⁰ – 10¹¹ Дж, а в каждой молнии длительностью до 0,1 с, обычно выделяется энергия 10⁷ - 10¹⁰ Дж (до нескольких тонн тротила). При ударе молнии в землю разряд происходит в полях около 3 кВ/см, что на порядок меньше пробойного поля для воздуха. Сначала идет лидер с током около 100 А, потом от земли обратный разряд. Эта главная стадия молнии с током до 100 кА, температурой Т ≈ 25 – 30 кК и скоростью 0,1 – 0,3 от скорости света вызывает ударную волну, действие которой сопровождается громовыми раскатами. Воздействие гроз опасно для наземных объектов и летательных аппаратов. Поэтому полезна разработка методов, позволяющих моделировать действие молнии и грома на различные объекты и совершенствовать средства грозовой защиты.

В [2,3] разработаны методы и проведено моделирование действия рентгеновского излучения на стенки взрывных камер импульсных ядерных энергетических установок. В [4] получены критерии моделирования молнии разрядом конденсаторных батарей из определяющих модельные и натурные процессы МГД уравнений. В [5] определены параметры РГД процессов для различных взрывчатых веществ (ВВ). Ниже приведены результаты исследований и разработки методов моделирования грозовой активности на наземные объекты и летательные аппараты разрядом конденсаторных батарей, импульсным лазерным облучением и взрывом с энергией до 100 кДж характерной для гроз в средних широтах.

 Постановка опытов

При моделировании электрическим разрядом применялась батарея конденсаторов емкостью до 13000 мкФ, напряжением до 5 кВ, запасаемой энергией до 160 кДж. При разряде батареи через плоский проводник возникал электрический взрыв, плазменное облако которого моделировало плазму молнии, а ударная волна (УВ) гром. Облучение преград лазерами с взрывной накачкой на длине волны 1,315 мкм позволяло увеличить плотность подводимой энергии. Большая энергоемкость мощных ВВ упрощала моделирование действием УВ и излучения взрыва. Для моделирования влияния бури на параметры УВ и плазмы применялся внешний обдув.

Скоростные фотокамеры с разных направлений регистрировали плазменный факел. Калориметры, фотодиоды, пироэлектрические и термопарные датчики измеряли радиационные и тепловые потоки. Пьезоэлектрические датчики и импульсомеры регистрировали параметры УВ. Электрический ток i, напряжение U, длительность t₀ и электрическая энергия E_э разряда измерялись поясом Роговского и делителем напряжения. Для измерения параметров лазерного излучения применялся специальный измерительный комплекс. Кроме стандартных методов поверки и тарировки измерительной аппаратуры использовалось действие УВ и излучение взрыва.. Выделение энергии разряда, облучения или взрыва ВВ проводилось на малые мишени, на плоские преграды и на входе в воздухозаборник (ВЗ) летательного аппарата (ЛА).

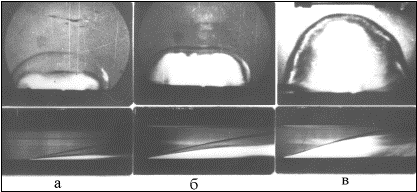Рис.1. Характерные фото разрядного факела и его щелевые развертки у поверхности плоской преграды при плотностях потока q выделенной в разряде энергии 0,6 (а); 3(б); 9 МВт/см² (в).

На рис. 1 а, б, в приведены отдельные кадры высокоскоростных фотографий разрядов у поверхности плоской преграды к моменту окончания разряда и их щелевые развертки для различных значений плотности выделения энергии q, характерных для молниевой плазмы. С ростом q зона энерговыделения догоняла фронт УВ. При q ≈ 3 МВт/см² они практически совпадают. На рис 2 показана постановка опытов на конусе у входа в воздухозаборник самолета. Видна фольга – инициатор разряда.

Для определения энергии плазмы необходимой для нарушения работы двигателя в условиях полета на низких высотах и дозвуковых скоростях проводились модельные опыты с внешним обдувом струей выхлопных газов другого ЛА.

Рис. 2. Слева - воздухозаборник летательного аппарата. Справа разряд на конусе у входа в воздухозаборник вид сбоку, время слева направо и сверху вниз, между кадрами 13,5 мкс. Внизу затекание плазмы разряда в воздухозаборник. Вид спереди, время между кадрами 330 мкс. Энергия разряда Е_э = 18 кДж, Частота работы двигателя n = 93% от максимальной.

При разработке критериев моделирования применялись общие для модели и натуры МГД уравнения [1,5] и безразмерные критерии моделирования:
π = P_m/P₀, λ = R/(E/P₀)^1/3, сI/P₀(E/P₀)^1/3, сτ/(E/P₀)^1/3, L/R. Здесь P_m/P₀ – отношение максимального давления УВ к атмосферному, E – энергия плазмы, I, τ – удельный импульс и длительность положительной фазы УВ, с - скорость звука, L, R характерный размер разряда и расстояние до него. Размерный критерий j²/σ определяет равенство удельных мощностей энерговклада в молнии и в разряде батареи. Условие (- div q) = (j²/σ) определяет равенство удельных мощностей энерговклада в лазерной плазме и молнии, где j – плотность тока, σ - проводимость плазмы, q – плотность потока поглощенной в плазме энергии излучения. Теплота взрыва тротила и ТГ 50/50 в экспериментах Q = 4,2 и 4,87 МДж/кг, E = GQ, G - масса ВВ Полученные критерии позволили по данным модельных экспериментов и расчетов определять действие гроз на различные объекты и совершенствовать средства грозозащиты.

Результаты

Некоторые результаты измерений параметров УВ и облака плазмы при разрядах , лазерном облучении и взрывах при атмосферном давлении с энергией характерной для молний приведены в таблицах и на рисунках. На рис. 3 показаны безразмерные зависимости ∆π (λ) приращения максимального давления от безразмерного расстояния λ, определяющие модельные и натурные процессы в сферической УВ. Светлыми и черными ромбами показаны результаты измерений при лазерном облучении и разрядах. Сплошными и пунктирными линиями показаны расчеты Brode [6] для сферического взрыва тротила и нагретой сферы.

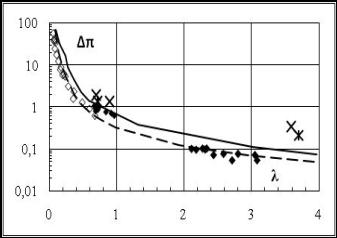Рис.3. Зависимости приращения безразмерного давления ∆π на фронте сферической УВ от приведенного расстояния λ в воздухе. Сплошными и пунктирными линиями показаны расчеты Brode для сферического взрыва тротила и нагретой сферы [6]. Светлые и черные ромбы - измерения при лазерном облучении и разрядах. Большие кресты и звезды - измерения при разрядах и скорости внешнего обдува 80 и 40 % от максимальной 200 м/с.

Зависимости ∆P_m(R/G^1/3) и I/G^1/3(R/G^1/3) для максимального давления и удельного импульса УВ при взрыве тротила описываются формулами Садовского (1) совпадающими с расчетами Броуда при R/G^1/3 ≥ 1 для сферического взрыва тротила

∆P_m= 0,084/(R/G^1/3) + 0,27/(R/G^1/3)² + 0,695/(R/G^1/3)³, I =184//(R/G^2/3) (1),

где давление ∆P_m на фронте УВ в МПа, расстояние R в м, G масса тротила в кг [4,7]. Теплота взрыва тротила принята Q = 4,2 МДж/кг, E = GQ, R/G^1/3 = 3,47λ = 3,47R/(E/P₀)^1/3. Средние значения тротилового эквивалента разряда ТЭ = 0,27 и 0,34 для максимального давления и удельного импульса УВ получены сравнением результатов измерений с расчетами по формулам (1) для взрыва тротила. При сравнении с расчетами (пунктир на рис. 3) для взрыва горячей сферы, практически совпавшими с опытными данными, ТЭ = 1. Параметры УВ при внешнем обдуве на рис. 3 (кресты и звезды) для моделирования влияния бури на интенсивность грозы показали, что при скоростях обдува выше 100 м/с давление может возрастать более, чем вдвое, а ТЭ на порядок.

При сравнении расчетов параметров сферической УВ для ВВ с измерениями при разрядах на плоских преградах, выделившаяся энергия по данным специальных взрывных экспериментов, полагалась равной E = 2(E_э – E_e), а при разрядах на конусе E = 1,75(E_э– E_e), где E_э – энергия разряда, E_e = 3 кДж/г - энергия нагрева фольги инициатора разряда до пробоя воздуха. При лазерном облучении плоскости и конуса энергия взрыва в воздухе полагалась соответственно равной E = 2E_л и E = 1,75E_л, где E_л – энергия лазерного излучения, поглощенная в плазме.

В таблице 1 приведены некоторые результаты измерений параметров разрядной и лазерной плазмы на конусе ЛА в 10 см от входа в ВЗ после окончания выделения энергии и результаты измерений в ВЗ, где E - полная энергия плазмы с учетом энергии горения фольги, E_э – энергия разряда, m - масса фольги, h и V₁ - высота подъема и объем факела на преграде к концу выделения энергии, I – удельный импульс, переданный преграде. T_я,ик - яркостная температура плазмы в ИК области. Внутри ВЗ измерялись ∆P_0,5, ∆P₃ и ∆P_6,4 – приращения давления УВ на расстояниях 0,5; 3 и 6,4 м от входа в ВЗ, t_пр – время прихода УВ к датчику, L и U - длина и скорость области нагретого газа, ∆T_{м 6,4}, ∆T_{ср 6,4} – максимальная и средняя температуры области нагретого газа, на расстоянии 6,4 м от входа в ВЗ, которая приходит после УВ, n₁% - частота работы двигателя в % от максимальной 200 м/с.

Таблица 1. Параметры разрядной и лазерной плазмы перед и внутри воздухозаборника летательного аппарата с работающим двигателем.

	Разрядная плазма					Лазерная плазма
№	46	47	60	50	49	1	2	3	4
E, кДж	35	27	16,6	19	14	23	19,5	18	30
Eэ, кДж	31	22,7	16,4	15	10,4	-	-	-	-
m, г	0,14	0,14	0,005	0,14	0,14	-	-	-	-
h, см	21	18	-	14	11,5	-	-	11,5	21
V1, литр	52	42	-	26	20	31	29	-	-
Tя,ик, кК	27,5	21	-	22	21	-	-	-	32
I, Пас	5	3,5	-	2,8	2,1	3,9	2,5	3,2	5,4
∆P0,5, МПа	0,2	0,22	-	0,4	0,17	0,17	0,14	-	0,17
tпр, мс	1	1	-	0,95	1	1	1,1	-	-
∆P3, МПа	0,04	0,037	-	0,036	-	0,045	-	-	0,067
tпр, мс	6	6	-	5,6	-	5,9	-	-	5,4
∆P6,4, МПа	0,01	0,01	-	-	0,009	0,012	-	-	0,013
tпр, мс	13,2	12,6	-	-	15	13	-	-	12
L, м	1,5	1,6	-	1,45	1,5	1,1	1,25	1,45	1,3
U, м/с	130	157	-	150	157	146	153	152	170
∆Tм 6,4, K	53	68	-	78	35	48	82	44	85
∆Tср 6,4, K	30	34	-	29	19	27	50	20	60
n1%	80	92,2		92,2

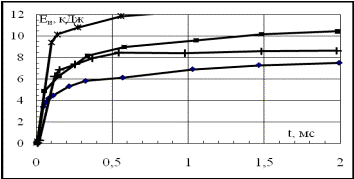
На рис. 4 показаны зависимости приведенных объемов разрядной, лазерной плазмы и продуктов взрыва ВВ от приведенного времени. На рис.5 показаны зависимости энергии излучения Е_и от времени t, а на рис.6 зависимости относительной энергии излучения E_и/E от приведенного времени t/E^1/3 при разрядах и облучении.

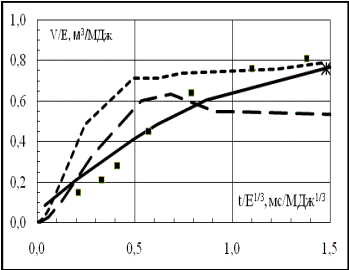Рис. 4. Зависимости приведенных объемов V/E прдуктов взрывных процессов от приведенного времени t/E^1/3. Мелкий пунктир - взрыв 11 г смеси 50/50 литого тротила с гексогеном [5]. Крупный пунктир - расчет Броуда взрыва тротила [6]. Сплошная линия - расчет Броуда для изотермы 3 кК взрыва горячей сферы [6]. Звезда – характерное значение V₁/E для молнии после окончания разряда. Квадраты – разряд на конусе с энергией E = 32 кДж при неработающем двигателе (n₁= 0).

Приращение энергии газа в факеле после расширения до атмосферного давления ∆E_г = (P₀V₁/(k₁-1)) – (P₀V₁/(k₀-1)) = 2,5 P₀V₁. При k₁ = C_p/C_v =1,2; P₀ = 0,1 МПа, ∆E_г/E_э= 2,5 P₀(0,91+29 m/E_э) = 0,23+7,2 m/E_э.
Рис.5. Зависимость энергии излучения Е_и от времени t при разрядах и облучении. Звезды и кресты - лазеры, опыт № 4, E = 30 кДж и опыт № 3, Е = 18 кДж. Ромбы и квадраты – разряды, опыт № 49, E = 14 кДж и опыт № 50, Е = 19 кДж.

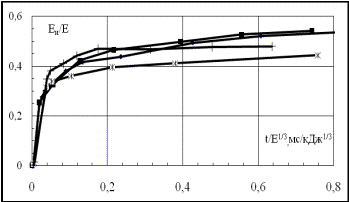
Рис.6. Зависимости относительной энергии излучения E_и/E от приведенного времени t/E^1/3 при разрядах и облучении. Обозначения как на рис. 5.

По данным датчиков давления на расстояниях 0,5; 3,4 и 6,4 м от входа в ВЗ на рис. 7а,б построены зависимости приращения максимального безразмерного давления УВ от приведенных расстояний ∆π(r/Е^1/2) внутри ВЗ при разных энергиях плазмы и скоростях вращения ротора двигателя от n = 0 до n = 0,93. С увеличением n давление ∆π существенно возрастает. На рис. 7б приведена зависимость ∆π от расстояния R1/Е^1/2 при R1= r (1-n*0,59) в ВЗ в координатах учитывающих сокращение пути УВ в движущемся в ВЗ газе. При этом 0,59 = 200/340 - отношение максимальной скорости продувки при n = 1 к скорости звука. Все данные на рис.7 б ложатся на общую зависимость, что подтверждает сделанное предположение.

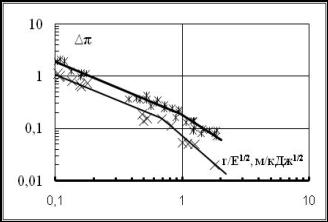
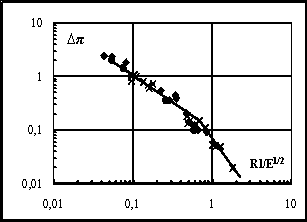
Рис.7а,б. Зависимости приращения ∆π максимального давления УВ от приведенного расстояния в м/кДж^1/2 внутри воздухозаборника при частотах вращения двигателя
n = 0 - крест, n = 0,7 – звезды, n = 0,8 – круг, n = 0,93 –ромб. r – расстояние УВ от разряда. R1 = r (1 - n*0,59) учитывает снос УВ потоком. E – энергия, вложенная в факел.

Обсуждение результатов

В [8] приведены результаты измерения параметров проходящих УВ в трубах при взрывах на входе в трубу на ее оси, которые описываются эмпирическими формулами, учитывающими потери на трение на стенках труб.

∆P_м = (0,79E_k/L + 0,39 (E_k/L)^0,5)*exp(-0,004L/r_т ); J = 1000∆P_мτ/2 ; τ в мс = L в м. (1а)

где ∆P_м и J - максимальное давление и удельный импульс УВ в МПа и Пас, L в м расстояние от входа в трубу до УВ, r₀ и r_т - расстояние от заряда до трубы и ее радиус. E_k = E/2πr_т² при r₀ = 0 или E/4πr_т² при r₀ >> r_т. В общем случае
E_k = (E/2πr_т²)((r₀² + r_т²)^1/2 - r₀)/(r₀ ² + r_т ²)^1/2). Здесь E_k в МДж/м²- энергия УВ в конусе входящая в трубу, E - энергия взрыва на расстоянии r₀ от трубы на вершине конуса в МДж.

На рис. 8 показаны зависимости ∆π (L/E_k) в УВ внутри ВЗ при частоте вращения двигателя n = 0. Кресты и линия - данные измерений при разряде и их тренд. Пунктир - расчет взрыва ВВ по формуле (1а) для трубы постоянного сечения, где не учтен тротиловый эквивалент разряда ТЭ = 0,27. Это завышает его результаты по сравнению с данными для разряда. Наличие излома на зависимостях ∆π (L/E_k) на рис.7а,.б и рис.8 вызвано торможением УВ расширяющимся конусом в ВЗ до расстояния 3 м. ВЗ представлял трубу диаметром около 0,7 и длиной около 7 м с конусом длиной около 3 м на входе трубы, проходное сечение которой убывало до расстояния L= 3 м, а потом резко возрастало за конусом.

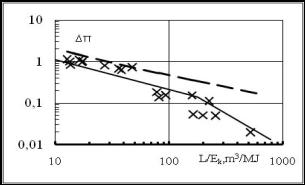Рис.8. Зависимости приращения максимального давления УВ ∆π от приведенного расстояния L/E_k внутри ВЗ при частоте вращения двигателя n = 0. Пунктир расчет [8] по формуле (1 а). Кресты и линия данные измерений и их тренд.

Результаты измерения объемов V₁ плазмы на конусе после окончания разряда приведенных на рис.4 и таблице 1, можно описать эмпирической формулой
V₁/E_э = 0,91+29 m/E. При m/E_э ~ 0, V₁/E_э = 0,91, что близко к расчету Броуда [6] для объема ограниченного изотермой 3 кК, для которой V₁/E около 0,75 м³/МДж. Измеренная доля энергии излучения после окончания разряда при малых энергиях горения фольги E_и/E_э = 0,4 - 0,5. При больших m/E_э излученная энергия могла превышать энергию разряда (E_и/E_э >1). В среднем, увеличение объема плазмы за счет горения фольги около 30 л/г или м³/кг. Если пренебречь энергией 3кДж/г для нагрева фольги до разряда, то баланс энергии при разряде можно написать в виде
E = E_э + E_гор = E_ув + E_и + ∆E_г, где E_э и E_гор выделившаяся энергии электрического тока и горения, E_ув - энергия уносимая УВ, ∆E_г энергия нагретого газа при атмосферном давлении. Измерения параметров факела при разряде показали, что при
m/E_э > 4*10^-3г/кДж, E_ув = 0,35(E_э – E_e) = 0,35E_э –1,05m, где E_e/m = 3кДж/г. Энергия газа в факеле после высвета - ∆E_г = 0,23+7,2 m, E_и = 0,53+19 m - энергия излучения,
E = 1,1 E_э +21 m -энергия факела. При m/E_э < 4 10^-3г/кДж, E_и = 0,45+37 m, E = E_э + E_гор = E_ув + E_и + ∆E_г = 1,03 E_э +38,3 m. Когда m = 0, E = 1,03E_э баланс энергии выполнялся и близок к балансу для облучения и при воздействии молнии, для которой принималось E_ув /E_м = 0,35, ∆E_г/E_м = 0,23, E_и /E_м = 0,45, где E_м – энергия молнии.

Измерения параметров плазмы при разряде, облучении, взрыве и модельные исследования воздействия молнии на газотурбинные двигатели в ЛА типа МИГ- 21 проводились при разных частотах работы двигателя n₁ от 0 до 93 % от максимальной. Плазма создавалась на конусе перед входом в ВЗ двигателя ЛА. Определялись условия нарушения газодинамической устойчивости двигателя по результатам измерений параметров плазмы перед и внутри ВЗ. Схема модельных опытов с разрядом показана на рис. 2. Диаграмма, определяющая энергетическую границу срыва газодинамической устойчивости двигателя ЛА при разных частотах его работы n₁ показана на рис. 9 для разрядной плазмы. В опытах с подчеркнутыми значениями энергии в таблице 1 происходил помпаж (заглохание) двигателя. При минимальной энергии разрядной плазмы E = 14 кДж нарушений в работе двигателя не наблюдалось. Модельные опыты показали, что срыв в работе ГТД наступал после прохождения УВ и области нагретого газа, носил вероятностный характер и зависел от энергии или объема плазмы и числа оборотов двигателя.

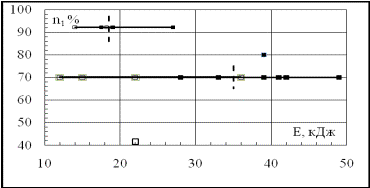Рис.9. Диаграмма, характеризующая энергетическую границу срыва газодинамической устойчивости двигателя ЛА при разрядах и разных частотах его работы n₁. Темные и светлые квадраты – помпаж и его отсутствие. Вертикальный пунктир граница срыва.

Нарушения в работе двигателя сопровождались выбросом нагретого газа навстречу потоку в ВЗ. Моделирование действия молнии на ЛА летящие на низких высотах и дозвуковых скоростях меньше 500 км/час внешним обдувом показало, что такой обдув не влияет на газодинамическую устойчивость двигателя ЛА.

Энергия молний оценивалась по их светящимся фотографиям диаметром от 0,1 до 1 м. На рис. 3 сплошной кривой приведена зависимость приведенного объема V/E от приведенного времени t/E^1/3 ограниченного изотермой T/T₀ = 10 (T₀ = 300 К) при взрыве горячей сферы [6], по которой оценивалась энергия молнии. Звезда - приведенный эквивалентный объем молнии V₁/E = 0,75 м³/МДж, принятый равным максимальному удельному объему молнии после пробоя ограниченному изотермой. V₁ = π R₁²×h = 3,14м³ при радиусе R₁ = 1м участка высотой h = 1м для цилиндрической симметрии. Удельная энергия молнии E = 4 МДж/м. Время от начала разряда t = 35 мс. Молния с характерной длиной 4 км будет иметь энергию E = 4* 4000 = 16000 МДж или около 4000 кг тротила. При радиусе R₁ = 5 см энергия молнии будет 39,3 МДж или в 400 раза меньше.

В таблице 2 приведены расчеты давления ∆P_m, удельного импульса I и длительности УВ в воздухе τ при разряде молний длиною L = 4 км с энергиями E = 4200 и 39,3МДж между 2 облаками по формулам для цилиндрического взрыва тротила [7] при ТЭ = 0,27 и атмосферном давлении

∆P_m = 1020(q/R²) + 200(q^3/8/R^3/4); I = 397(q^3/4/R^1/2); τ = 2I/∆P_m (2),

где R в м расстояние до молний, ∆P_m в кПа, I в Пас, масса зарядов G = 270 и 0,558 кг q = G/L= 0,0675 и 0,00014 кг/м, теплота взрыва тротила Q = 4,2 МДж/кг.

Таблица 2. Параметры УВ в воздухе при пробое молнии длиной 4 км с энергией E = 4200 МДж (1000 тонн ТНТ) и 39,3 МДж между 2 облаками.

R, км	0,001	0,01	0,1	1	2	4
E = 4200 МДж
∆Pm, кПа	141,6	13,6	2,31	0,41	0,24	0,14
I, Пас	52,6	16,6	5,26	1,66	1,18	0,83
τ, мс	0,74	2,44	4,55	8,12	9,66	11,5
E = 39,3 МДж
∆Pm, кПа	7,2	1,3	0,23	0,04	0,024	0,014
I, Пас	0,511	0,162	0,051	0,016	0,011	0,008
τ, мс	0,142	0,253	0,450	0,801	0,952	1,133

Давление ∆P_m на фронте УВ на расстоянии L = 4 км из таблицы 2 было сравнено с результатами измерений, влиянием высоты пренебрегалось. При разряде с E = 39,3 МДж, ∆P_m = 14 Па, u_m= 7 мкм/с удовлетворительно согласуется с измеренным в [9] значением u_m ≈ 5 мкм/с.

Разработанные методы моделирования действия молний на ЛА предполагается усовершенствовать для целей над облаками, когда молнии, бьющие в ионосферу при низком давлении атмосферы имеют характерные особенности [10], которые надо учитывать при моделировании.

Заключение

Разработаны методы моделирования и проведены модельные исследования действия гроз на наземные объекты и низколетящие летательные аппараты взрывом, разрядом и облучением, с критериями моделирования основанными на общих, определяющих модельные и натурные процессы МГД уравнениях. Измеренные параметры УВ и облака плазмы при взрывах, разрядах и лазерном облучении с энергией характерной для молний в средних широтах, сопоставлены с результатами их измерений при взрывах ВВ и взрывных расчетах, определены их тротиловые эквиваленты. Проведены оценки характерных параметров молнии и грома, получено согласие с результатами сейсмологических измерений действия молний на полигоне. Проведено моделирование действия молнии на двигатели летательных аппаратов и определены параметры плазмы, приводящие к нарушению их газодинамической устойчивости на низких высотах. Разработанные методики применялись при отработке противопомпажных систем летательных аппаратов и средств грозозащиты.

Литература

1. Базелян Э.М., Райзер Ю.П. Физика молнии и молниезащиты. М.: Физматлит. 2001.

2. Соловьёв В.О., Христофоров Б.Д.. Моделирование действия рентгеновского излучения на стенки взрывных камер импульсных ядерных энергетических установок // Физика горения и взрыва. 2008. № 5(44). С.123 -129.

3. Соловьев В.О., Христофоров Б.Д. Моделирование воздействия рентгеновского излучения на ячеистую структуру стенок камеры ЯЭУ // Атомная энергия. 2008. № 1 (105). С. 32-37

4. Христофоров Б.Д. Моделирование газодинамических процессов при грозах мощными электрическими разрядами // Физика горения и взрыва. 2010. № 1 (46). С. 11-19.

5. Христофоров Б.Д. Параметры радиационно - газодинамических процессов в воздухе при наземных, приземных и воздушных взрывах зарядов ВВ массой до 1000 тонн // Физика горения и взрыва. 2014. № 1(50). С.107 - 114.

6. Броуд Г. Расчеты взрывов на ЭВМ. Газодинамика взрывов. М.: Мир. 1976. 271 с.

7. Гельфанд Б.Е., Сильников М.В. Барометрическое действие взрывов. СПб, Издательсво Астерион. 2006.

8. Khristoforov B. Investigation of Shock Wave Parameters at Explosives Blasts in the Tubes with Air // Universal Journal of Engineering Science. 2013. (2). с. 28-33, http://www.hrpub.org DOI: 10.13189/ujes.2013.010202.

9. Санина И.А., Рыбнов Ю.С., Солдатенков А.М. и др. Сейсмоакустические эффекты при грозовой активности//Геофизика межгеосферных взаимодействий. М.: ГЕОС. 2008. С. 67- 78.

10. Pasko V.P., Stanley M.A., Matthews J.D., Inan U.S., Wood T.G. Electrical discharge from a thundercloud top to the lower ionosphere // Nature. 2002. V. 416. P. 152-154.