Технические науки/2. Механика

 

К.т.н Кабаков А.М, к.т.н, Мамаев Л.М., к.т.н, Романюк А.Д.,

к.т.н, Телипко Л.П.

Днепродзержинский Государственный технический университет, Украина

ВЛИЯНИЕ ДИССИПАТИВНЫХ СИЛ НА КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ МЕХАНИЗМА ПОДЪЕМА КРАНА

 

Рассмотрим систему дифференциальных уравнений, описывающую свободные колебания системы со многими степенями свободы, которая в матрично-векторном виде будет:

                                                          (1)

где ,  и  - квадратные симметричные матрицы.

Задача состоит в том, чтобы на базе доступной информации о коэффициентах поглощения y или логарифмических декрементах gотдельных  упругодиссипативных элементов найти достоверные, с позиций инженерного расчета, значения элементов  диссипативной матрицы . Некоторые пути решения этой задачи с разных позиций рассмотрены в работах [1,2,3].

Пренебрегая влиянием диссипативных сил, перейдем от обобщенных координат  к нормальным  с помощью линейного преобразования:

                                        ,                                                     (2)

где - квадратная матрица, составленная из векторов собственных форм колебаний консервативной системы. Используя ортогональность собственных форм относительно инерционной  и квазиупругой матриц:

, 

                                    при                                    (3)

где приходим к системе в главных координатах:

                                                             (4)

где  - соответственно диагональные матрицы обобщенных коэффициентов инерции и жесткости

                .                             (5)

Уравнение (4) можно записать в ином виде:

               ,                                 (6)

где  - квадраты частот собственных колебаний, - матрица обобщенных коэффициентов демпфирования:

                                        .                                        (7)

При слабой диссипации в уравнениях (4) можно пренебречь всеми не диагональными элементами матрицы , то есть воспользоваться допущением о том, что диссипативные связи между формами колебаний отсутствуют (между формами колебаний не происходит «перекачки»  энергии, обусловленной нелинейными диссипативными силами). Таким образом, мы налагаем условия ортогональности собственных форм и по отношению к диссипативной матрице :

                          ,        при .                                 (8)

Условиям ортогональности (8) удовлетворяет матрица вида (2):

,

где  и - произвольные постоянные.

При диагональной матрице каждой форме колебаний соответствует некоторый  обобщенный коэффициент поглощения :

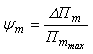                   ,                                                      (9)

где  и - рассеянная и максимальная потенциальные энергии цикла, соответствующе «m» -ой форме колебаний. Величина  легко определяется на базе известных коэффициентов поглощения  отдельных упругодиссипативных элементов. Тогда элементы матрицы :

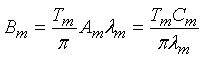                             ,                                (10)

где обобщенный логарифмический декремент колебаний:

                                .                                               (11)

Элементы матрицы  в соответствии с зависимостью (7):

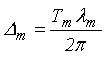                                 .                                          (12)

По известной матрице  находится искомая матрица  коэффициентов сопротивлений:

                    .                                        (13)

Для практических расчетов формулу (13) можно упростить, так как обращение матрицы  требует большого объема вычислений. Для этого используются условия ортогональности собственных форм колебаний (3). Так как

    

то, умножая слева на обращенные матрицы масс и жесткостей, получим:

 

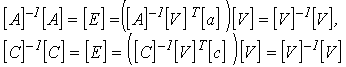
откуда

                                                   (14)

Подставляя выражения (14) в формулу (13), найдем:

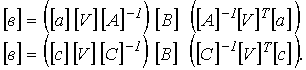
Вследствие симметричности матриц   и  можно записать, что

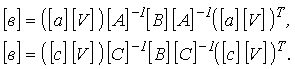
Так как результат перемножения трех диагональных матриц дает диагональную матрицу с элементами:

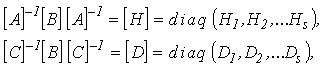
где

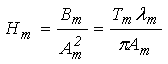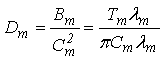,      ,                   (15)

то выражение (13) запишется в виде:

                                            (16)

                        .                       (17)

По сравнению с формулой (13) одна операция обращения и две умножения матриц заменены в выражениях (16) и (17) на три операции умножения. Определив   еще более упрощается, если одна из матриц -  или   диагональные.

В главных координатах решение системы уравнений (6) имеет вид:

                                              (18)

где  и   - начальное смещение и фазовый угол, определяемые из начальных условий,  - частота колебаний диссипативной системы:

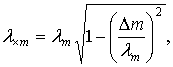 которую с достаточной степенью точности можно принимать равной частоте колебаний консервативной системы. Время затухания колебаний по каждой из собственных форм:

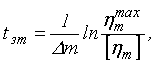
где  и - соответственно максимальная и допускаемая амплитуды колебаний в каждой из собственных форм. Полагая, что , получим с учетом выражения (12)

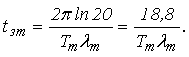
Таким образом, в качестве меры рассеяния энергии при свободных колебаниях многомассовых систем могут использоваться время затухания колебаний   по каждой из собственных форм и обобщенные коэффициенты поглощения .

Литература:

1. Динамический  расчет зданий и сооружений М.Ф.Берштейн, В.А.Ильчев, Г.Коренев  и др., Под редакцией Б.Г. Коренева, И.М.Абрамовича. - М.: Стройиздат,1984.-303с.- (Справочник проектировщика).

2.     Клаф Р., Пензиен Дж. Динамика сооружений: Пер. с англ. М.: Стройиздат,1979.-320с.

3.     Коловский М.З. Динамика машин.- М.: Машиностроение,1989.-263 с.