Лимаренко А.М., Давид М.А., Балтянский И.В.

(Одесский национальный политехнический университет, Украина)

Моделирование и Расчет металлоконструкции поперечины металлорежущего станка портального типа

В современных условиях все большую значимость в машиностроении приобретают вопросы повышения точности и производительности станочного парка при одновременном снижении материалоемкости оборудования.

Решение этих задач связано с поисками новых конструктивных форм и усовершенствованием существующих. Современное состояние вычислительной техники и, что особенно важно, наличие мощного программного обеспечения позволяют решать вопросы жесткости и точности обработки, которые раньше были обозначены только в теоретическом плане.

В настоящее время широкое распространение в расчетной практике имеют численные методы. Применение этих методов особенно эффективно для конструкций со сложной геометрией, с разрывами физико-механических свойств материала, при сложных граничных условиях. Одним из наиболее распространенных численных методов на сегодня является метод конечных элементов (МКЭ), который предполагает явную аппроксимацию решения на малых подобластях – конечных элементах.

Целью данной работы является расчет поперечины специализированного сверлильно-расточного станка ОС-4037. Для этого использована программа ANSYS, реализующая метод конечных элементов.

Аппроксимация модели выполнена оболочечным конечным элементом Shell181 из библиотеки конечных элементов программы ANSYS.

Этот конечный элемент определяется как многослойная оболочка с конечными деформациями, имеет четыре узла с шестью степенями свободы в каждом из них: перемещения в направлениях осей X, Y, Z узловой системы координат и углы поворотов вокруг этих осей.

Конечно-элементная модель поперечины содержит 8653 элементов и 8843 узлов. При моделировании поперечины дополнительно схематически смоделирован шпиндельный блок, где учтены основные габаритные размеры (рис.1). Интенсивность вертикальной распределенной нагрузки соответствует весу шпиндельного блока (каретка, пиноли, проставки, шпиндели, коробка скоростей с узлами привода главного движения, механизмы отжима и зажима инструмента).

При рассмотрении поперечины ее основание крепилось в местах соединения со стойками станка. Здесь накладывается запрет осевых смещений в направлении осей X, Y, Z, и углов поворотов вокруг этих осей.

На рисунке 1 представлена расчетная модель поперечины.

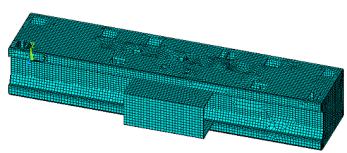
Рис.1. Расчетная модель поперечины

Анализ напряженно-деформированного состояния поперечины выполнен по величинам эквивалентных напряжений и полных перемещений. Максимальные эквивалентные напряжения по гипотезе Губера-Мизеса составили 32 МПа (рис.2), а полные перемещения – 141мкм (рис.3).

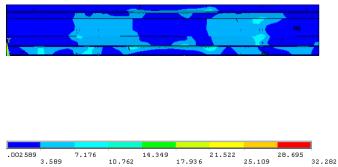
Рис.3. Эквивалентные напряжения

Рис.3. Полные перемещения

Характер распределения этих величин по длине поперечины неодинаков и имеет ярко выраженные максимумы в середине пролёта. В связи с этим представляется целесообразным оптимизировать конструкцию поперечины. Очевидна необходимость ужесточения средней её части. Предложенная методика расчета позволяет на стадии проектирования определять жесткость элементов несущих систем металлорежущих станков и давать рекомендации по их конструкции.

Литература

1. Дащенко О.Ф., Розрахунок напружено-деформованого стану станини гідропреса / О.Ф. Дащенко, В.Д. Ковальов, О.М. Лимаренко – Праці Одеського політехнічного університету, 2012, Вип.2., с. 35-43.

2. Оробей В.Ф., Метод граничних елементів в задачах з нестійкими розв'язками / В.Ф. Оробей, О.Ф. Дащенко, О.М. Лимаренко – Праці Одеського політехнічного університету, 2013, Вип.2., с. 27-31.

3. Боряк К.Ф., Перевірка на міцність конструктивних елементів ЗНКП-60 К.Ф. Боряк, О.В. Афтанюк, О.М. Лимаренко. Збірник наукових праць Одеської державної академії технічного регулювання та якості – 2015. – №2 (7)

4. Лимаренко О.М. Розрахунок телескопічної стріли автомобільного крану. / О.М. Лимаренко, Дащенко О.О., Лимаренко А.С. – Science and civilization 2015 – Construction and architecture Physics Technical sciences, England, Sheffield № 24 с. 69-73