Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

ВЛИЯНИЕ пяти ПЕРЕМЕННЫХ НА построение графиков V_u и V_L

В представленной ниже статье рассмотрен вопрос влияния пяти переменных на такие параметры как Vu и Vl, которые изображены одновременно на двухмерных рисунках. Они позволяют более полно представить влияние различных переменных сразу на два параметра. При этом переменные могут увеличиваться, уменьшаться и быть постоянными. То есть, в предлагаемой статье рассмотрены зависимости изменения Vu (Vl) = f(Х1, Х2, Х3, Х4, Х5).

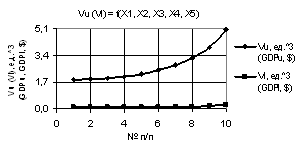
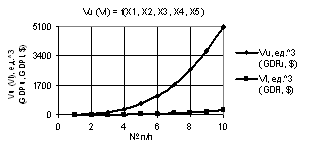
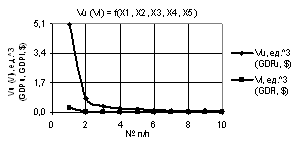
На первом рис. 1 показаны зависимости Vu и Vl при Х1 = Х2 = Х3 = Х4 = 1, Х5 = 0.1…1. Из данного рисунка видно, что значения Vu и Vl увеличиваются, причем более интенсивно увеличивается параметр Vu.

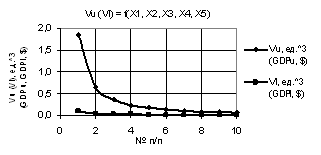
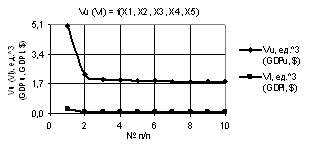
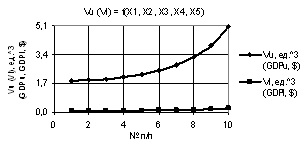
Рис. 1. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х2 = Х3 = Х4 = 1, Х5 = 0.1…1	Рис. 2. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = 1, Х2 = Х3 = Х4 = 1…10, Х5 = 0,1…1
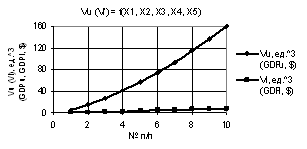
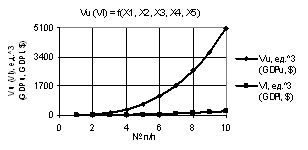
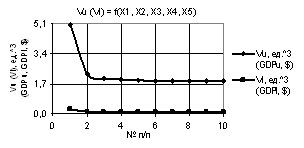
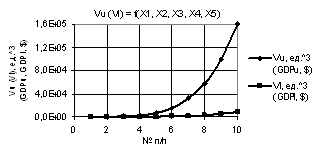
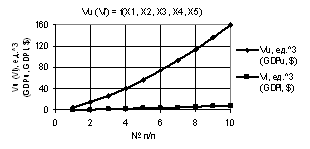
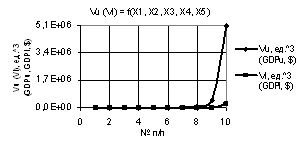
Рис. 3. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = 1…10, Х2 = Х3 = Х4 = Х5 = 1	Рис. 4. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х2 = 1…10, Х3 = Х4 = Х5 = 1

Следующий рис. 2 дает наглядное представление, что при значениях переменных Х1 = 1, Х2 = Х3 = Х4 = 1…10, Х5 = 0,1…1 построенные 2D зависимости Vu и Vl уменьшаются.

На следующих двух рисунках 3 и 4 показаны зависимости Vu (Vl) = f(X1, X2, X3, Х4), когда переменные были Х1 = 1…10, Х2 = Х3 = Х4 = Х5 = 1 и Х1 = Х2 = 1…10, Х3 = Х4 = Х5 = 1 соответственно. Здесь параметры Vu и Vl также увеличиваются, но на рис. 4 параметр Vu достигает значения 1,6Е+06.

Рис. 5. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х2 = Х3 = 1…10, 1, Х4 = Х5 = 1		Рис. 6. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 =Х2 = Х4 = 1…10, Х5 = 1
Рис. 7. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 = Х4 = Х5 = 1, Х2 = 1…10	Рис. 8. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х4 = Х5 = 1, Х2 = Х3 = 1…10

Следующие два рисунка 5 и 6 были построены при Х1 = Х2 = Х3 = 1…10, 1, Х4 = Х5 = 1 и Х1 = Х3 =Х2 = Х4 = 1…10, Х5 = 1. Из рисунков видно, что изображенная кривая Vu на рис. 5 достигает значений 5100, а на рис. 6 она резко уменьшается между точками 1 и 2 со значения 5,05 до 2,44 после чего достигает своего минимума 1,76.

Для построения двух 2D графиков на рис. 7 и 8 были использованы следующие значения переменных Х1 = Х3 = Х4 = Х5 = 1, Х2 = 1…10 и Х1 = Х4 = Х5 = 1, Х2 = Х3 = 1…10. На рис. 7 и 8 построенные кривые растут, достигая значений 5047 и 136 соответственно.

Из следующего рис. 9 видно, что кривые Vu и Vl уменьшаются, а на рис. 10 значения Vu растут до величины 5,05.

Рис. 9. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х5 = 1, Х2 = Х3 = Х4 = 1…10		Рис. 10. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 = 1…10, Х2 = Х4 = 1, Х5 = 0.1…1
Рис. 11. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 = Х5 = 1, Х2 = Х4 = 1…10	Рис. 12. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 = 1, Х2 = 1…10, Х4 = Х5 = 1…0,1

На последних двух рисунках 11 и 12 были построены две кривые Vu и Vl при Х1 = Х3 = Х5 = 1, Х2 = Х4 = 1…10 и Х1 = Х3 = 1, Х2 = 1…10, Х4 = Х5 = 1…0,1 соответственно.

Здесь на рис. 11 построенные кривые уменьшаются по аналогии с рис. 6. а на рис. 12 параметр Vu достигает больших значений 1.6Е+06.