Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

ПРЕДСТАВЛЕНИЕ ГРАФИКОВ Vu и VL в зависимости от пяти ПЕРЕМЕННЫХ

В данной статье рассмотрены варианты влияния пяти переменных на такие параметры как Vu и Vl, которые изображены одновременно на двухмерных рисунках, что позволяет более полно представить влияние различных переменных сразу на два параметра. При этом переменные могут увеличиваться, уменьшаться и быть постоянными. То есть, в предлагаемой статье рассмотрены зависимости изменения Vu (Vl) = f(Х1, Х2, Х3, Х4, Х5).

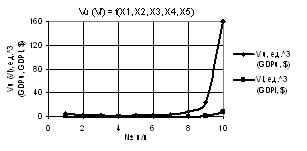
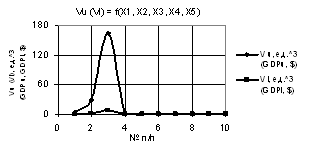
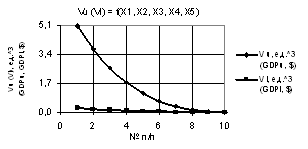
На первом рис. 1 показаны зависимости Vu и Vl при Х1 = Х2 = 1, Х3 = 1…10, Х4 = Х5 = 1…0.1. Поостренные кривые имеют минимумы 1.84 и 0.091 в точке 4.

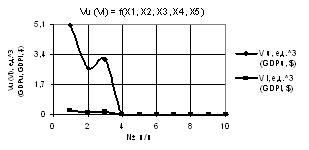
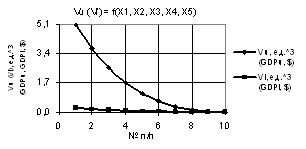
Рис. 1. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х2 = 1, Х3 = 1…10, Х4 = Х5 = 1…0.1	Рис. 2. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 =Х2 = 1,Х3 = 1…10,Х4 = 1…0.1,Х5 = 0.1…1
Рис. 3. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х5 = 1, Х2 = 1…10, Х3 = Х4 = 1…0.1	Рис. 4. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х5 = 1, Х2 = Х3 = 1…0.1, Х4 = 1…10

Следующий рис. 2 дает наглядное представление, что при значениях переменных Х1 = Х2 = 1, Х3 = 1…10, Х4 = 1…0.1, Х5 = 0.1…1 построенные 2D зависимости Vu и Vl также имеют минимумы 0.77 и 0.038 в точке 3.

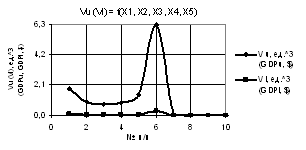
На следующих двух рисунках 3 и 4 показаны зависимости Vu (Vl) = f(X1, X2, X3, Х4), когда переменные были Х1 = Х5 = 1, Х2 = 1…10, Х3 = Х4 = 1…0.1 и Х1 = Х5 = 1, Х2 = Х3 = 1…0.1, Х4 = 1…10 соответственно. Здесь параметры Vu и Vl на рис. 3 также увеличиваются до максимума в точке 3 после чего падают до нуля. На рис. 4 параметр Vu резко снижается между точками 1 и 2 в 21 раз.

Рис. 5. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х5 = 1, Х2 = Х3 = 1…10, Х4 = 1…01		Рис. 6. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х5 = 1, Х2 = Х4 = 1…0.1, Х3 = 1…10
Рис. 7. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 = Х4 = Х5 = 1, Х2 = 1…10	Рис. 8. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 = 1…0.1, Х2 = 1…10, Х4 = Х5 = 1

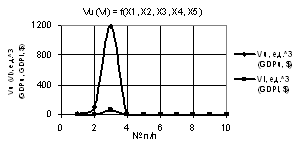
Следующие два рисунка 5 и 6 были построены при Х1 = Х5 = 1, Х2 = Х3 = 1…10, Х4 = 1…0.1 и Х1 = Х5 = 1, Х2 = Х4 = 1…01, Х3 = 1…10. Из рисунка 5 видно, что изображенная кривая Vu аналогична рис. 3 только ее максимальное значение равно 164.49. На рис. 6 построенные кривые Vu и Vl имеют минимумы 2.62 и 0.13 в точке 2.

Для построения двух 2D графиков на рис. 7 и 8 были использованы следующие значения переменных: Х1 = Х3 = Х4 = Х5 = 1, Х2 = 1…10 и Х1 = Х3 = 1…0.1, Х2 = 1…10, Х4 = Х5 = 1. На рис. 7 построенные кривые Vu и Vl также имеют минимумы 2.62 и 0.13 соответственно в точке 2. Из рис. 8 видно, что построенные кривые растут в 999.52 и 1000 раз соответственно.

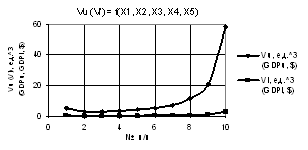
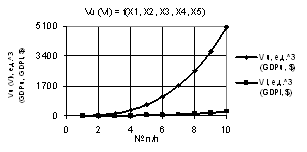
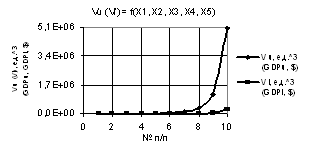
Из следующего рис. 9 видно, что кривые Vu и Vl уменьшаются, а на рис. 10 значения Vu растут до значительной величины 5.05Е+06.

Рис. 9. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 = 1…10, Х2 = 1…0.1, Х3 = Х4 = 1		Рис. 10. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х2 = 1…10, Х3 = 0.1…1,Х4 = Х5 = 1
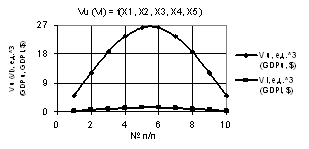
Рис. 11. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = 1…0.1, Х2 = Х3 = 1…10, Х4 = Х5 = 1	Рис. 12. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х2 = Х3 = 1…0.1, Х4 = Х5 = 1

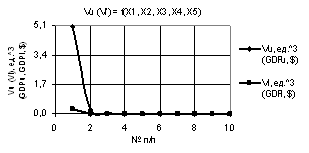
На последних двух рисунках 11 и 12 были построены две кривые Vu и Vl при Х1 = 1…0.1, Х2 = Х3 = 1…10, Х4 = Х5 = 1 и Х1 = Х2 = Х3 = 1…0.1, Х4 = Х5 = 1 соответственно.

Здесь на рис. 11 построенные симметричные кривые имеют максимумы 26.23 и 1.3 в точках 5 и 6 соответственно.

На рис. 12 рассчитанные параметры кривых Vu и Vl уменьшаются в 505 и 1000 раз соответственно.