Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

Анализ построенных графиков Vu и VL с использованием пяти переменных

Ниже представлена статья, в которой рассмотрены двенадцать вариантов влияния пяти переменных на параметры Vu и Vl. Построенные кривые Vu и Vl изображены одновременно на рисунках совместно, что позволяет более полно представить влияние различных переменных сразу на два параметра. При этом переменные могут увеличиваться, уменьшаться и быть постоянными. Таким образом, в предлагаемой статье рассмотрены зависимости изменения Vu (Vl) = f(Х1, Х2, Х3, Х4, Х5).

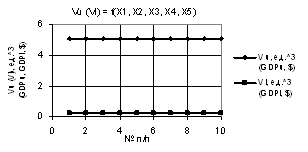
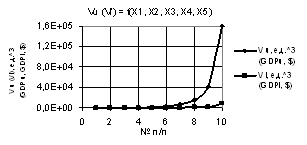
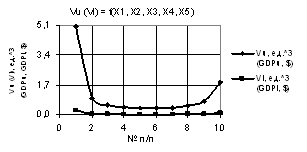
На первом рис. 1 изображены зависимости Vu и Vl при Х1 = Х4 = Х5 = 1, Х2 = 1…10, Х3 = 1…0.1. Из этого примера видно, что переменная Vu увеличивается значительно с 5.05 до 1.6Е+05, т.е. в 31683 раза.

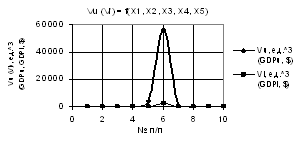
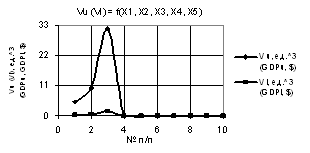
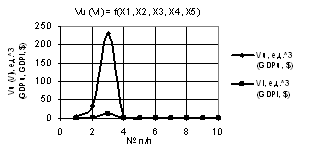
Рис. 1. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х4 = Х5 = 1, Х2 = 1…10, Х3 = 1…0.1	Рис. 2. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 =1,Х2 =1…10,Х3 = Х4 = 1…0.1,Х5 =0.1…1
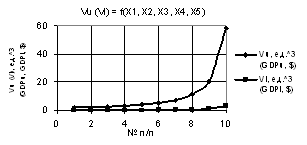
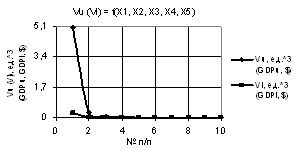
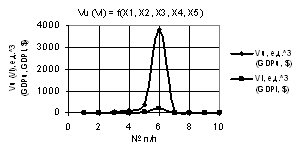
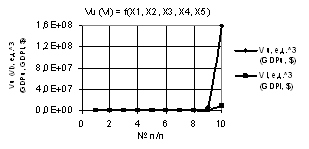
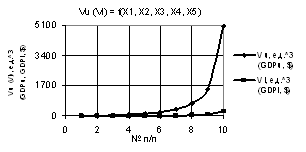
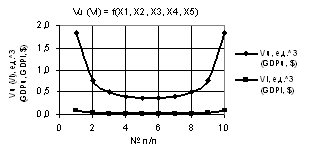
Рис. 3. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1=1,Х2=Х4=1…10, Х3=1..0.1,Х5=0,1…1	Рис. 4. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х5 =1, Х2 = Х3 = 1…0.1, Х4 = 1…10

Следующий рис. 2 показывает, что при значениях переменных Х1 =1, Х2 = 1…10, Х3 = Х4 = 1…0.1, Х5 = 0.1…1 построенные зависимости Vu и Vl растут скачкообразно начиная с точки 6 достигая своего максимума, например Vu до 56231, т.е. увеличившись в 30411 раз, после чего падают до нуля.

На следующих двух рисунках 3 и 4 показаны зависимости Vu (Vl) = f(X1, X2, X3, Х4, Х5), когда переменные были Х1 = 1, Х2 = Х4 = 1…10, Х3 = 1...0.1, Х5 = 0,1…1 и Х1 = Х5 =1, Х2 = Х3 = 1…0.1, Х4 = 1…10. Здесь параметры Vu и Vl на рис. 3 увеличиваются незначительно до 56 и 3 соответственно. На рис. 4 параметр Vu достигает самого большого значения 1.6Е+08 увеличившись в 1.02Е+06 раз.

Рис. 5. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 = 1…10, Х2 = Х4 = Х5 = 1		Рис. 6. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 = 1…10, Х2 = Х5 = 1, Х4 = 1…0.1
Рис. 7. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х3 = Х4 = 1…10, Х2 = Х5 = 1	Рис. 8. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = 1…10, Х2 = Х4 = Х5 = 1, Х3 = 1…0.1

Следующие два рисунка 5 и 6 были построены при Х1 = Х3 = 1…10, Х2 = Х4 = Х5 = 1 и Х1 = Х3 = 1…10, Х2 = Х5 = 1, Х4 = 1…0.1. Из рисунка 5 видно, что параметры Vu и Vl, при данных значениях переменных, остаются величинами постоянными. Кривые, представленные на рис. 6, растут до своего максимума в точке 3 после чего падают до нуля.

Для построения двух 2D графиков на рис. 7 и 8 были использованы следующие значения переменных: Х1 = Х3 = Х4 = 1…10, Х2 = Х5 = 1 и Х1 = 1…10, Х2 = Х4 = Х5 = 1, Х3 = 1…0.1. На рис. 7 построенные кривые Vu и Vl резко уменьшаются между точками 1 и 2. Из рис. 8 видно, что построенные кривые начинают быстро расти после точки 6.

Из следующего рис. 9 видно, что кривые Vu и Vl имеют минимумы 0.36 и 0.0179 в точке 6. Построенные на рис. 10 кривые аналогичны рисункам 2 и 6, где кривые достигают своего максимума в точке 3, а после падают до нуля.

Рис. 9. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = Х4 = 1…10, Х2 = Х5 = 1, Х3 = 1…0.1		Рис. 10. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 = 1…10, Х2 = Х5 = 1Х3 = Х4 = 0.1…1
Рис. 11. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1 =1…10,Х2 =1,Х3=Х4 =1…0.1,Х5 = 0.1…1	Рис. 12. Vu (Vl) = f(X1, X2, X3, Х4, Х5) при Х1=Х4=1..10,Х2=1,Х3 = 1..0.1,Х5=0,1..1

На последних двух рисунках 11 и 12 были построены две кривые Vu и Vl при Х1 = 1…10, Х2 = 1, Х3 = Х4 = 1…0.1, Х5 = 0.1…1 и Х1 = Х4 = 1…10, Х2 = 1, Х3 = 1...0.1, Х5 = 0,1…1 соответственно.

Здесь рис. 11 аналогичен трем рисункам выше, где параметры Vu и Vl увеличиваются до своего максимума в точке 6, а после падают до нуля в точке 7.

На рис. 12 рассчитанные параметры кривых Vu и Vl имеют минимумы 0.36 и 0.018 в точках 5 и 6 .