Компьютерный поперечник в классе

Шынтаева С.Р.

Южно-Казахстанский государственный университет имени М.Ауезова, Шымкент, Казахстан

Аннотация:

Восстановление функций из классов Соболева в лебеговой метрике в контексте К(В)П в случае, когда информация об восстанавливаемой функции берется посредством всех возможных линейных функционалов с указанием оптимального вычислительного агрегата. Восстановление функций из классов Соболева по значениям в точках в лебеговой метрике в контексте К(В)П с указанием оптимального вычислительного агрегата. Были найдены оценки снизу при восстановлении любыми вычислительными агрегатами, построенными по информации, полученной от произвольного конечного набора линейных функционалов, при этом никакой речи об каком-либо конкретном способе приблеженного вычисления не шло. Только после всего этого было показано, что погрешности приближения Лагранжевыми сплайнами подтверждают неулучшаемость оценки снизу. В контексте Компьютерного (вычислительного) поперечника проведено полное исследование аппроксимативных возможностей интерполяционных многочленов Лагранжа, выяснены границы их неприминимости и эффективности.

Пусть даны числа такие что или Тогда при

выполнены соотношения

К(В)П-1:

(1)

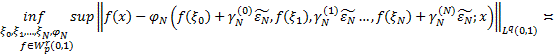
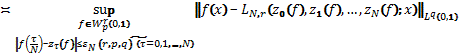К(В)П-2:

. (2)

Оценка снизу в (1) вытекает из леммы

где -поперечник по Гельфанду.

Перейдем к оценкам сверху по точной информации. В силу леммы при имеют место соотношения

(3)

откуда следует, что при оценка сверху в (3) совпадает с оценкой снизу в (1).

Опять же из (3) и леммы при здесь существенно используются то обстоятельство, что в лемме вычислительный агрегат не зависит и и неравенство следует

что завершает полное решение задачи К(В)П-1.

Литературы

References

1. Н.Темиргалиев. О задаче восстонавления по неточной информации //Вестник Евразийского национального университета.-2004-№1, 202-209 с.

2. Н.Бахвалов, Н.Жидков, Г.Кобельков. Численные методы. М.:Бином, 2007. 621-636 с .

3. Н.Темиргалиев, С.Кудайбергенов, А.Шоманова. Применение тензорных произведений функционалов в задачах численного интегрирования //Изв.РАН, сер.матем, (2009), 183-224 с.

4. К.Бабенко. Основы численного анализа. М.:Наука, 1986. 371-374 с.

5. Н.Темиргалиев. Компьютерный поперечник как синтез известного и нового в численном анализе //Вестник ЕНУ им.Л.Н.Гумилева, 2014, №101. 3-20 с.