Математика/1.Дифференциальные и интегральные уравнения

Дәулет Бақар

Абай атындағы ҚазҰПУ-нің магистранты

Қазақсан, Алматы қаласы

АНЫҚТАЛҒАН ИНТЕГРАЛДЫ ҚОЛДАНЫП, МАТЕМАТИКА ЖӘНЕ ФИЗИКА ЕСЕПТЕРІН ШЫҒАРУ

Анықталмаған интегралды есептеп шығару дегеніміз - берілген функция үшін, алғашқы образбен кез- келген тұрақты санның қосындысын табу болатын. Яғни, анықталмаған интеграл, еркімізше алынған тұрақты қосылғыштар дәлдігіне дейін анықталған, осының көмегімен көптеген есептер шешіледі. Енді біз, берілген функция үшін, алғашқы образдың өзін ғана емес, берілген a және b нүктелерінде алғашқы образдың мәндерінің айырмасын қарастырайық. Айталық, y=f(x) функциясының х[a; b] кесіндісіндегі алғашқы образдары F(x) пен Ф(x) болсын. Сонда алғашқы образдардың негізгі қасиеті бойынша, барлық х[a; b] үшін Ф(x) = F(x) + C

Болатындай тұрақты С болады. Демек, Ф(b)-Ф(a)=b нүктелерінде алғашқы образдың мәндерінің айырымын y=f(x) функциясы үшін алғашқы F(x) образының өсімшесі деп атайды. Сонымен, алғашқы образдың өсімшесі берілген f(x) функциясына және a мен b сандарына ғана тәуелді екен. Ал, көптеген есептердің шешуі алғашқы образдың өсімшесін есептеуге келіп тірелетін себепті, оған арнайы атау беріліп, өзгеше белгіленетін болады.

Мына жағдайды қарастырайық:

Анықтама. Дифференциалдау мен интегралдау амалдары өзара кері амалдар. Функцияның алғашқы функциясын табу операциясын интегралдау деп атайды.

y=f(x) функциясының a-дан b-ға дейінгі ([a; b] кесіндісіндегі) анықталған интегралы деп осы функцияның алғашқы F(x) образының өсімшесін (F(b) – F(a)) айтады да, мына түрде жазылады:

(1) Мұндағы, a мен b сандары интегралдау шектері (a- төменгі b- жоғарғы шегі) деп аталады. Ал f(x) функциясы – интеграл астындағы функция, x- интегралдау айнымалысы деп аталады.Үштары a мен b болатын [a; b] интегралдау кесіндісі деп аталады. Интегралдаудың жоғарғы шегі төменгі а шегінен үлкен болуы міндетті емес, яғни a>b және a=b болуы да мүмкін.

(1) формуланы Нютон – Лейбниц формуласы деп атайды.

Мысалы,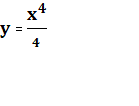 функциясы үшін алғашқы образ. Сондықтан

.

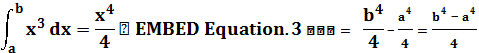1- Мысал. Материялық А нүктесі түзу бойымен қозғалып келеді

және оның [a; b] кесіндідегі кез-келген t уақыт мезетіндегі қозғалыс жылдамдығы v=v(t) болсын. А нүктесінің осы уақыт мезетіндегі орын ауыстыруы S- ті табайық.

Шешуі. Нүктенің х координатасы қозғалыс уақыты t-ның функциясы болады, яғни x=x(t). Олай болса, қозғалыс жылдамдығы екені белгілі.Бірақ А нүктесінің [a; b] уақыт аралығындағы орын ауыстыруы оның b және a уақыт мезеттеріндегі координаталарының айырымына тең, яғни

.

2- Мысал. Шешуі: ; ; .

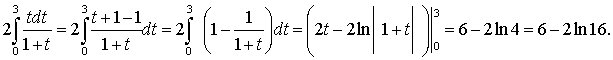
Бұл интегралды шығару барысында айнымалыны ауыстыру әдісін пайдаланамыз. Ереже бойынша, айнымалы ауыстырылса, онда интегралдау шектері де ауысатыны белгілі.

Айнымалы ауысқаннан кейін шыққан интеграл қарапайым интеграл. Оны интегралдау кестесін пайдаланып табуға болады.

Бұл жерде, ескерте кететініміз, айнымалыны дұрыс таңдау керек.

Қортындылай келгенде, біздің ұсынып отырғанымыз анықталған интеграл тақырыбына аса көніл бөлу керектігін айтқымыз келеді. Себебі, анықталған интегралды қолдану, әсіресе, инженер мамандықтар үшін аса қажетті.

Пайдаланылған әдебиеттер:

1. М.Асқарова. Туынды және интеграл., Алматы,1987. (90-91б)

2. Л.Х.Жунусова. Математика-1(оқу құралы). Алматы-2008. (104-105б).

3. А.Біргебаев. Жоғары математика элементтері. Алматы,2013. (108-110б)

4. Б.П.Демидович. Сборник задач и упражнений по математическому анализу., Москва «наука»,1990. (379-380б)

5. Е.Ж.Айдос., О.С.Сатыбалдиев. Жоғары математика III. Алматы, 2006. (49-50б)

6. Қ.Қабдықайыров,. Р.Есельбаева. Дифференциялдық және интегралдық есептеулер. Алматы,1985. (196-197)