Султанмуратова С., Апашев Д.

Южно-Казахстанский государственный университет им М.Ауезова

Дискретность спектра и полнота корневых векторов дифференциального оператора второго порядка с инволюцией

В пространстве рассмотрим спектральную задачу

, (1)

с комплекснозначным коэффициентом 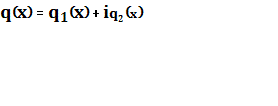. Преобразование в правой части равенства определен для любой функции равенством

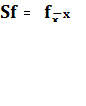
и называется инволюцией.

Действуя оператором к обеим частям равенства (1), получим уравнение

. (2)

Обозначим

. (3)

В работе [1] показано, что при число не является собственным значением спектральной задачи (1). Другими словами, уравнение

(4)

не имеет ненулевых решений из класса . Тем не менее, уравнение (4) имеет ненулевые решения: и . Нужно отметить, что эти утверждения справедливы и в случае уравнения (2).

Определим оператор с помощью дифференциального выражения (3) и множествa , элементами которого являются функции , удовлетворяющие следующим условиям:

1) функции абсолютно непрерывны вместе со своей первой производной на каждом конечном интервале числовой оси;

2) функция принадлежит классу

3) имеют место следующие соотношения

,

.

Итак, мы имеем дифференциальный оператор второго порядка с инволюцией , действие которого задается с помощью дифференциального выражения (3), с областью определения . На этот оператор можно распространить теоремы о дискретности спектра оператора и полноте корневых векторов, полученные в работе [1].

Т е о р е м а 1. Пусть функция ограничена снизу в каждом конечном интервале и выполнено условие

Тогда при любой мнимой части коэффициента оператор

имеет дискретный спектр.

Т е о р е м а 2. Пусть функция удовлетворяет условию

.

Тогда, для любого оператор

имеет дискретный спектр.

Аналог известного критерия дискретности спектра обыкновенного дифференциального оператора [2] формулируется в виде

Т е о р е м а 3. Пусть функция ограничена снизу, а функция - полуограничена. Тогда необходимым и достаточным условием дискретности спектра оператора

является выполнение условия

для любой последовательности непересекающихся интервалов одинаковой длины, когда интервал уходит в бесконечность.

Теперь сформулируем достаточные условия, при которых система собственных и присоединенных элементов оператора L является полной в . Полнота понимается в том смысле, что любая функция с наперед заданной точностью может быть в среднем квадратичном аппроксимирована некоторой конечной линейной комбинацией собственных и присоединенных функций.

Т е о р е м а 4. Пусть функция ограничена снизу, а функция - полуограничена, и пусть, кроме того, при некотором

. (23)

Тогда оператор обладает дискретным спектром и полной системой собственных и присоединенных функций.

Литература:

1. Лидский В.Б. Несамосопряжённый оператор типа Штурма-Лиувилля с дискретным спектром //Труды Моск. матем. общества. - I960. - № 9. - С. 45-79.

2. Молчанов А. М., Об условиях дискретности спектра самосопряженных дифференциальных операторов второго порядка, Труды Моск. матем. о-ва 2 (1953).