ПРАКТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА

ОБЪЕКТОВ УПРАВЛЕНИЯ ЭРГАТИЧЕСКИХ СИСТЕМ

Карев М.Н., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

При математическом описании сложных систем используются упрощения, состоящие в предположении линейности объекта в области малых изменений входящих в описание величин. При активных экспериментальных методах в процессе эксперимента создаются специальные воздействия на объект, которые вызывают изменения выходных координат (полезная информация, подлежащая обработке). Если используются пассивные методы, то специальные воздействия не предусматриваются и ограничиваются данными нормального функционирования. При решении практических задач определяются зависимости, в общих чертах правильно отражающие происходящие в объекте процессы. Что касается точности результатов, то, как правило, используется метод итераций. В основе анализа и синтеза изучаемых систем лежат динамические характеристики, которыми описывается поведение системы и отдельных ее элементов в переходных процессах (во время движения). Эти характеристики задаются в виде дифференциального уравнения или системы, кривых изменения выходной величины, при изменении входной величины определенной апериодической формы, частотной характеристики как функции . Первоначально определяются динамические характеристики отдельных элементов, а по ним находятся характеристики системы в целом. Возможен и другой подход к анализу и синтезу системы, когда сразу экспериментально определяются динамические характеристики системы в целом. В этом случае достигается большая достоверность получаемых характеристик. Основной недостаток – отсутствие данных о динамических характеристиках отдельных элементов. Обычно применяется поэлементное исследование регулирующей части системы, а объект исследования изучается в целом. Динамические связи между входными и выходными величинами определяются между каждым из m входов и n выходов. Все динамические свойства системы характеризуются характеристической матрицей . Погрешности, вносимые соседними входными величинами, можно значительно уменьшить, если во время эксперимента осуществлять их стабилизацию около выбранных значений и непрерывно вести регистрацию для проверки их стабильности. Во избежание нарушения режима функционирования объекта и обеспечения линейности системы большие отклонения выходных величин не допускаются. Для получения достоверных данных необходимо, чтобы отклонения при испытаниях не превышали максимальных отклонений при регулировании (обычно определяется требованиями к системе).

Отметим, используемые в экспериментах приборы обычно не являются идеальными усилительными звеньями. Поэтому реально в ходе испытаний вместо , определяются , ; вместо кривых , будут получены кривые , . Естественно, приборы должны быть подобраны так, чтобы их инерционностью можно было пренебречь по сравнению с инерционностью объекта; в зоне пропускаемых объектом частот приборы должны быть близки к усилительному звену:

, .

При измерениях выходной величины рационально использовать прибор, который предполагается использовать как входное устройство регулятора, а возмущение по каналу регулирующих воздействий наносить регулирующим органом, например, с помощью исполнительного механизма. Желательно, чтобы шкалы приборов по измерению входных и выходной величин были равномерными.

Указанный подход к анализу и синтезу систем использовался при разработке тренажеров как сложных технических устройств, с определенной степенью точности еалиизующих математическую модель реального объекта. Здесь изменение состояния объекта на временном интервале с хорошим приближением описывается системой обыкновенных дифференциальных уравнений. В нормальной форме Коши:

,

(1)

- вектор состояния, - вектор управления, - матрицы параметров объекта. Поведение вектора может быть произвольным. Ход управляемого процесса определяется на некотором интервале , если на этом интервале вектор задан в виде . Вектор-функция определяет программное управление; вектор-функцией определяется закон управления. При заданных начальных условиях уравнение (1) имеет решение

,

(2)

; .

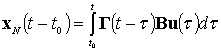Таким образом, движение объекта описывается уравнением (1) в некоторой области изменения параметров, определяемой эксплуатационным диапазоном его применения. Решение системы (1) в виде (2) характеризует опорные траектории, соответствующие заданным начальным условиям при выбранном векторе управления . Соотношением определяется подобие тренажера имитируемому реальному объекту. Для оценки точности воспроизведения характеристик объекта в тренажере можно пронормировать в виде , где - характеристики, полученные в результате натурных испытаниях объекта; - расчетные характеристики объекта при тех же начальных условиях в соответствии с (1).

Предложенные подходы использовались при разработке обучающих комплексов для подготовки операторов транспортных систем [1].

Литература

1. Гарькина И.А., Данилов А.М., Прошин И.А. Тренажеры модульной архитектуры для подготовки операторов транспортных систем / XXI век: итоги прошлого и проблемы настоящего плюс. - 2013. - № 12 (16). - С. 37-42.