С.И. Куликов, А.И. Нестеренко, Н.Г. Нестеренко

ГВУЗ “ Украинский государственный химико-технологический университет”

г. Днепропетровск

К вопросу повышения точности аппроксимации граничного условия при решении двумерной задачи Стефана в многосвязной области

Математические модели таких важных проблем физики, как распад твёрдых растворов, рост и залечивание пор, конденсация и испарение, рост островковых плёнок и др., представляют собой задачу Стефана в многомерной многосвязной постановке. Существующие численные методы не позволяют получить достаточно точное решение этой задачи с явным выделением границы раздела фаз. Основная трудность состоит в том, что в результате движения межфазных границ изменяется область решения задачи, т.к. появляются новые, ранее принадлежащие другой фазе узлы пространственной сетки, в которых не определено значение сеточной функции. В [1] авторами сформулирована математическая модель диффузионного взаимодействия ансамбля частиц, случайно расположенных в пространстве. Здесь же приведен оригинальный метод вспомогательной сетки и нетрадиционный способ определения модуля градиента сеточной функции. Однако при практической реализации алгоритма решения сформулированной задачи возникают проблемы, связанные с обеспечением высокой локальности определения градиента сеточной функции (концентрации) на межфазной границе, а также с повышением точности аппроксимации граничного условия задачи Стефана. В [2] рассматривается первая из этих проблем и предлагается способ её разрешения. В данной работе приводится решение второй проблемы.

Пусть по истечении временного полушага граница не пересекает узлов сетки. В этих случаях уравнение диффузии записывается на неравномерной сетке и, как результат, точность его аппроксимации порядка (), что ниже точности метода Кранка-Никольсона (К.Н.), для которого точность порядка (). Здесь некоторые константы (шаги пространственно-временной сетки). В результате этого неточности определения сеточной функции вблизи межфазной границы приводят к локальному искажению формы последней, появлению нефизичных «петель» и «провалов».

В соответствии с [3], повышения точности аппроксимации второй производной на неравномерной сетке можно добиться увеличением точек аппроксимации. Используя это, рассмотрим наиболее сложную ситуацию, когда вторые производные ( и горизонтальная, и вертикальная ) аппрксимируются на неравномерной сетке (рис.1, в,г)

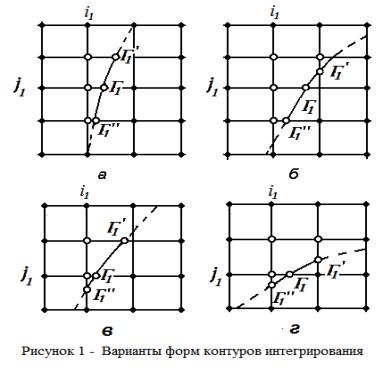
Здесь - граница -й частицы,

- коордтнаты пересечения -й межфазной границы с горизонталью и вертикалью соответственно

Уравнение диффузии аппроксимируется схемой К.Н. и, записанное на регулярных узлах, имеет вид ( в предположении, что коэффициент диффузии не зависит от концентрации)

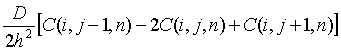+ (1)

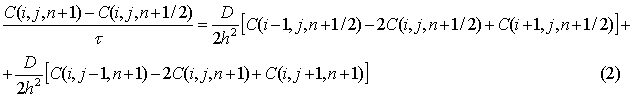
Запишем (1) для узла () (рис.1, в,г) с учётом разностной аппроксимации второй производной повышенной точности [3]:

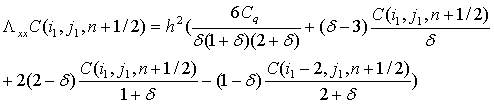
где - безразмерное расстояние от границы раздела фаз до узла () по линии прогонки :

Тогда имеем

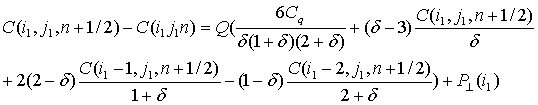(3)

Здесь - перпендикулярная к линии прогонок производная, вычисляемая по явной схеме:

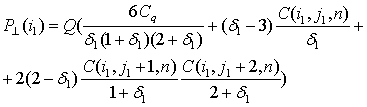
Где - безразмерное расстояние от границы раздела фаз до узла () по линии, перпендикулярной линии прогонки : ,

Дополним (3) уравнением диффузии в узле ():

,

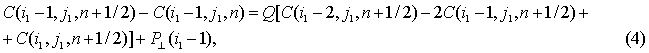
Здесь определяется по трём точкам: (), (), (), если , и по четырём точкам: , (), (), (), если .

Подставив , определённое из (3), в (4), окончательно получим для организации горизонтальной прогонки искомое граничное условие в точке () точности :

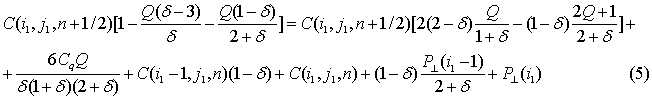
Аналогично можно получить граничное условие и при организации вертикальной прогонки.

Исследуем уравнение (5) в предельных случаях.

Пусть , при этом межфазная граница попадает в узел (). Возникающую неопределённость вида можно раскрыть умножением (5) на . Тогда после предельного перехода имеем , что совпадает с граничным условием метода «ловли границы в узел сетки».

При граница попадает в узел (), тогда (5) принимает вид что эквивалентно уравнению диффузии (4), записанному в узле () и являющемуся граничным условием метода «ловли границы в узел сетки».

Следовательно, уравнение (5) имеет точность порядка и локальность записи, достаточную для решения многомерных задач Стефана, и полностью описывает граничное условие на межфазных границах.

Литература

1. Kulikov S.I., Nesterenko A.I., and Nesterenko N.G., A design of reactionary diffusion is in the two-demensional systems. 5th international scientifically practical conference “Basic directions of modern science – 2009”, Sofia (Bulgaria), 18,36-41,2009

2. Куликов С.И., Нестеренко А.И., Нестеренко Н.Г. Особенности решения двумерной задачи Стефана. Сборник «Прикладные задачи математики и механики.». Материалы ХIX международной научно-технической конференции., г. Севастополь, 12-16 сентября 2011 г.,с.151-155.

3. Марчук Г.И., Шайдуров В.В. Повышение точности решений разностных схем. М., 1979.